如图,在四边形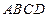 中,
中,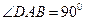 ,
, ,
,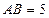 ,
, ,
,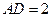 ,求四边形
,求四边形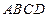 绕
绕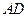 旋转一周所成几何体的表面积及体积.
旋转一周所成几何体的表面积及体积.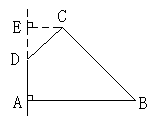
已知椭圆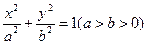 的离心率
的离心率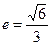 ,
,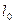 为过点
为过点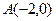 和上顶点
和上顶点 的直线,下顶点
的直线,下顶点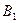 与
与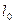 的距离为
的距离为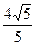 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆的动弦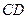 交
交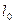 于
于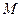 , 若
, 若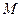 为线段
为线段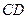 的中点,线段
的中点,线段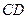 的中垂线和x轴交点为
的中垂线和x轴交点为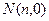 ,试求
,试求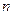 的范围.
的范围.
如图,
已知正三棱柱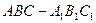 的底面边长是2,D是侧棱
的底面边长是2,D是侧棱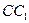 的中点,平面ABD和平面
的中点,平面ABD和平面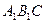 的交线为MN.
的交线为MN.
(Ⅰ)试证明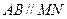 ;
;
(Ⅱ)若直线AD与侧面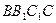 所成的角为
所成的角为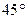 ,试求二面角
,试求二面角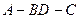 的大小.
的大小.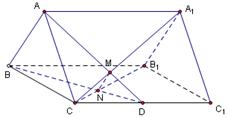
袋子里有大小相同的3个红球和4个黑球,今从袋子里随机取球.
(Ⅰ)若有放回地摸出4个球,求取出的红球数不小于黑球数的概率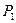 ;
;
(Ⅱ)若无放回地摸出4个球,
①求取出的红球数ξ的概率分布列和数学期望;
②求取出的红球数不小于黑球数的概率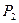 ,并比较
,并比较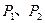 的大小.
的大小.
设平面上向量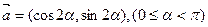 ,
,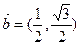 ,
,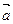 与
与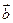 不共线,
不共线,
(Ⅰ)证明向量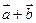 与
与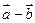 垂直;
垂直;
(Ⅱ)若两个向量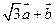 与
与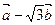 的模相等,试求角
的模相等,试求角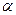 .
.
如图,在四边形ABCD中,AD=8,CD=6,AB=13,∠ADC=90°,且 .
.
(1)求sin∠BAD的值;
(2)设△ABD的面积为S△ABD,△BCD的面积为S△BCD,求 的值.
的值.
 |