古希腊人常用小石子在沙滩上摆成各种形
状来研究数。比如： 
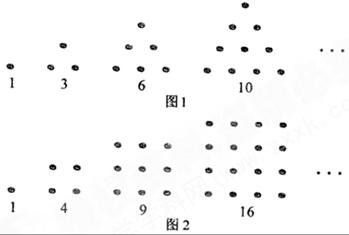
他们研究过图1中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数；类似的，称图2中的1，4
，9，16，…这样的数为正方形数。下列数中既是三角形数又是正方形数的是（ ）
| A．299 | B．378 |
C．1024 | D．1225 |
已知直线
平行，则k的值是（）
| A． 1或3 | B．1或5 | C．3或5 | D．1或2 |
已知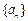
为等差数列，
，
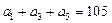。以
表示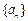的前n项和，则使得达到最大值的n是 （）
（A）21（B）20（C）19（D）18
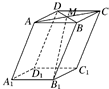
如图，在底面ABCD为平行四边形的四棱柱ABCD－A1B1C1D1中，M是AC与BD的交点，若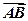
＝
，
＝
，
＝
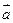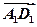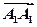，则下列向量中与
相等的向量是 ( )
| A．－＋＋ |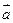
B．＋＋ |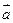
| C．－＋ |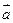
D．－－＋ |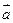
设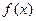
为定义在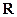
上的奇函数，当
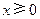时，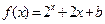
(
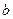为常数)，则
（）
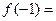| A．3 | B．1 | C．-3 | D． |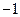
设A＝{x|x2－2x－3＞0}，B＝{x|x2＋ax＋b≤0}，若 A∪B＝R，A∩B＝(3,4]，则a ＋b等于 ( )
| A．7 | B．－1 | C．1 | D．－7 |