((本小题14分)
已知函数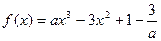
(I)若函数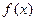 在
在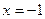 时取得极值,求实数
时取得极值,求实数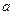 的值;
的值;
(II)试讨论函数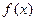 的单调性;
的单调性;
一个半径为1的小球在一个棱长为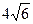 的正四面体容器内可向各个方向自由运动,则该小球永远不可能接触到的容器内壁的面积是.
的正四面体容器内可向各个方向自由运动,则该小球永远不可能接触到的容器内壁的面积是.
设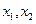 是
是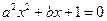 的两实根;
的两实根;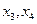 是
是 的两实根。若
的两实根。若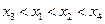 ,则实数
,则实数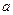 的取值范围是;
的取值范围是;
在等腰梯形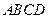 中,
中,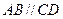 ,且
,且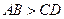 。设以
。设以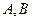 为焦点且过点
为焦点且过点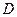 的双曲线的离心率为
的双曲线的离心率为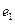 ,以
,以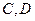 为焦点且过点
为焦点且过点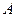 的椭圆的离心率为
的椭圆的离心率为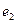 ,则
,则 =;
=;
已知 函数f(x)=|x2-2|,若f(a)≥f(b),且0≤a≤b,则满足条件的点(a,b)所围成区域的面积为;
函数f(x)=|x2-2|,若f(a)≥f(b),且0≤a≤b,则满足条件的点(a,b)所围成区域的面积为;
.如图,平面 平面
平面 ,
, =直线
=直线 ,A,C是
,A,C是 内不同的两点,B,D是
内不同的两点,B,D是 内不同的
内不同的
两点,且A,B,C,D 直线
直线 ,M,N分别是线段AB,CD的中点。下列判断正确的是;
,M,N分别是线段AB,CD的中点。下列判断正确的是;
①.当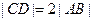 时,M,N两点不可能重合
时,M,N两点不可能重合
②.M,N两点可能重合, 但此时直线AC与
但此时直线AC与 不可能相交
不可能相交
③.当AB与CD相交,直线AC平行于 时,直线BD可以与
时,直线BD可以与 相交
相交
④.当AB,CD是异面直线时,直线MN可能与 平行
平行