观察 ,
,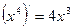 ,
, ,由
,由 归纳推理可得:若定义在
归纳推理可得:若定义在 上的函数
上的函数 满足
满足 ,记
,记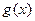 为
为 的导函数,则
的导函数,则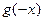 =
=
A. |
B.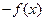 |
C.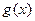 |
D. |
已知函数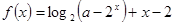 ,若
,若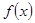 存在零点,则实数
存在零点,则实数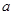 的取值范围是()
的取值范围是()
A.(-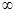 ,-4 ,-4 ∪[4,+ ∪[4,+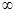  |
B.[1.+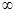 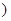 |
C.[2, +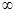 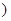 |
D.[4, +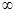 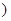 |
下列四种说法中,错误的个数是()
①A={0,1}的子集有3个
②“若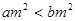 ,则
,则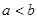 ”的逆命题为真
”的逆命题为真
③“命题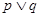 为真”是“命题
为真”是“命题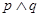 为真”的必要不充分条件
为真”的必要不充分条件
④命题“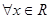 ,均有
,均有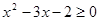 ”的否定是:“
”的否定是:“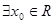 ,使
,使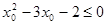 ”
”
| A.0个 | B.1个 | C.2个 | D.3个 |
已知 是奇函数,
是奇函数, 是偶函数,且
是偶函数,且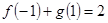 ,
, ,则
,则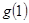 =()
=()
| A.4 | B.3 | C.2 | D.1 |
函数 ,若函数
,若函数 在区间(
在区间( ,
, +1)上单调递增,则实数
+1)上单调递增,则实数
的取值范围是()
A.(- ,1 ,1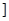 |
B.[1, 4] |
C.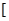 4, + 4, + ) ) |
D.(- ,1 ,1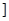 ∪[4, + ∪[4, + ) ) |
设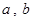 是两条不同的直线,
是两条不同的直线,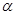 ,
, 是两个不同的平面,则能得出
是两个不同的平面,则能得出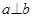 的是()
的是()
A.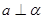 , ,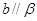 , ,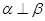 |
B.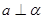 , ,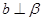 , ,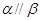 |
C.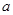 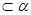 , ,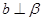 , ,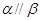 |
D.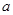 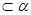 , ,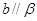 , ,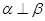 |