.某商店在1-10月份的时间销售A、B两种电子产品,已知产品A每个月的售价 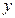 (元)
(元)
与月份 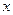 (
( 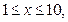 且
且 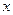 为整数)之间的关系可用如下表格表示:
为整数)之间的关系可用如下表格表示:
时间 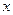 (月) (月) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
售价 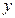 (元) (元) |
720 |
360 |
240 |
180 |
144 |
120 |
120 |
120 |
120 |
120 |
已知产品A的进价为140元/件,A产品的销量 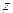 (件)与月份
(件)与月份 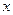 的关系式为
的关系式为 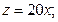 已知B产品的进价为450元/件,产品B的售价
已知B产品的进价为450元/件,产品B的售价 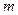 (元)与月份
(元)与月份 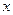 (
( 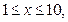 且
且 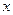 为整数)之间的函数关系式为
为整数)之间的函数关系式为 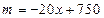 ,产品B的销量
,产品B的销量 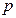 (件)与月份
(件)与月份 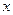 的关系可用如下的图像反映.
的关系可用如下的图像反映.
已知该商店每个月需固定支出500元的物管杂费以及5个员工的工资,已知员工每人每月的工资为1500元.请结合上述信息解答下列问题:
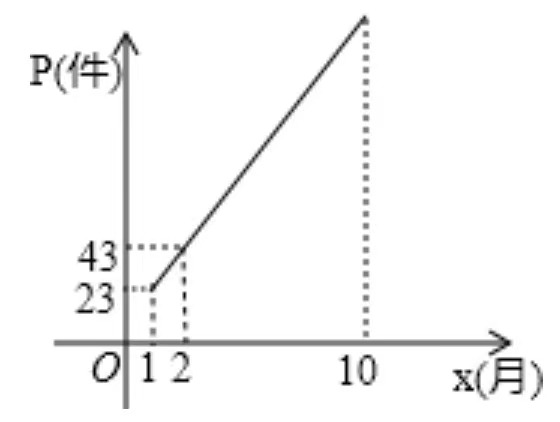
(1)请观察表格与图像,用我们所学习的一次函数,反比例函数,或者二次函数写出 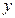 与
与 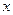 的
的
函数关系式, 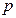 与
与 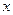 的函数关系式;
的函数关系式;
(2)试表示出商店每月销售A、B两种产品的总利润 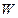 (将每月必要的开支除去)与月份
(将每月必要的开支除去)与月份 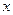 的
的
函数关系式,并求出该商店在哪个月时获得最大利润;
(3)为了鼓励员  工的积极性,在最后4个月的销售期间商店老板决定奖励员工,除了正常的
工的积极性,在最后4个月的销售期间商店老板决定奖励员工,除了正常的
工资外,每卖一件A产品,每个员工都提成0.75元,每卖一件B产品每个员工都提成10
元,这样A产品的销量将每月减少 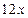 件,而B产品的销量将每月增加
件,而B产品的销量将每月增加 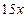 件;请问在第几月时总利润(除去当月所有支出部分)可达到16750元?
件;请问在第几月时总利润(除去当月所有支出部分)可达到16750元?
(参考数据: 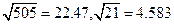 )
)
已知矩形ABCD,长BC=12cm,宽AB=8cm,P、Q分别是AB、BC上运动的两点。若P自点A出发,以1cm/s的速度沿AB方向运动,同时,Q自点B出发以2cm/s的速度沿BC方向运动,问经过几秒,以P、B、Q为顶点的三角形与△BDC相似?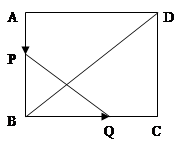
升国旗活动时,某同学站在距旗杆27米的地方,当五星红旗冉冉升起时,同学行注目礼,五星红旗升至旗杆顶端时测得该同学视线的仰角为30°,已知该同学身高1.5米,你能计算出旗杆的高度吗?请你先画出示意图,再写出计算过程(结果用根式表示)。
A市气象发报,一沙尘暴中心在A市正西方向1000Km的B处,正迅速向北偏东65°的方向沿BC移动,距沙尘暴400Km范围内为受沙尘暴影响区域,请你用学过知识说明A市是否受沙尘暴影响?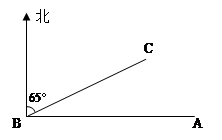
将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,如图,设筷子露出在杯子外面长为hcm,则h的取值范围是什么?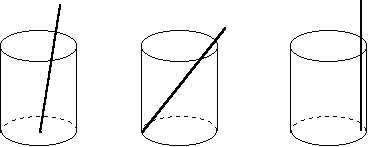
将长为38cm,宽为5cm的长方形白纸,按如图所示方法粘合在一起,粘合部分白纸为2cm。
(1)求10张白纸粘合后的长度;
(2)设x张白纸粘合后的总长为ycm,写出y与x的函数关系式。