如图一,平面四边形ABCD关于直线AC对称, ,
, ,
, 。
。
把 沿BD折起(如图二),使二面角A-BD-C的余弦值等于
沿BD折起(如图二),使二面角A-BD-C的余弦值等于 。对于图二,
。对于图二,
(1)求 的长,并证明:
的长,并证明: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值。
所成角的正弦值。
在 中,
中,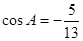 ,
, .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)设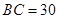 ,求
,求 的BC边上的中线AD的长.
的BC边上的中线AD的长.
(本小题满分12分) 已知等差数列 的前n项和为
的前n项和为 ,且
,且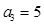 ,
, .
.
(Ⅰ)求数列 的通项
的通项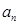 ;
;
(Ⅱ)设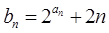 ,求数列
,求数列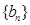 的前n项和
的前n项和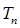 .
.
设过点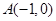 的直线
的直线 与过点
与过点 的直线
的直线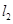 相交于点M,
相交于点M,
且 与
与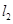 的斜率
的斜率 ,
,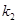 的乘积为定值
的乘积为定值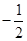 ,求点M的轨迹方程.
,求点M的轨迹方程.
选修4-5:不等式选讲
已知函数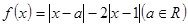 .
.
(Ⅰ)当a=3时,求函数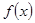 的最大值;
的最大值;
(Ⅱ)解关于x的不等式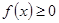 .
.
选修4-4:坐标系与参数方程
在直角坐标系xOy中,直线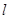 的参数方程为
的参数方程为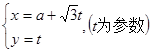 .在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
.在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为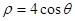 .
.
(Ⅰ)求圆C在直角坐标系中的方程;
(Ⅱ)若圆C与直线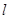 相切,求实数a的值.
相切,求实数a的值.