如图,四面体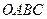 的三条棱
的三条棱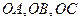 两两垂直,
两两垂直,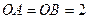 ,
,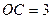 ,
,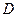
为四面体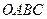 外一点.给出下列命题.
外一点.给出下列命题.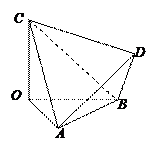
①不存在点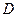 ,使四面体
,使四面体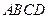 有三个面是直角三角形;
有三个面是直角三角形;
②不存在点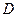 ,使四面体
,使四面体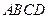 是正三棱锥;
是正三棱锥;
③存在点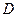 ,使
,使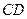 与
与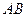 垂直并且相等;
垂直并且相等;
④存在无数个点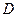 ,使点
,使点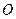 在四面体
在四面体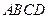 的外接球面上.
的外接球面上.
其中真命题的序号是 .
.如图所示,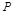 为
为
 所在平面上一点,且
所在平面上一点,且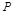 在线段
在线段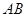 的垂直平分线上,若
的垂直平分线上,若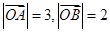 ,则
,则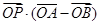 的值为( )
的值为( )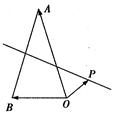
| A.5 | B.3 | C. |
D.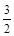 |
已知在等差数列 中
中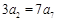 ,
,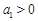 ,则下列说法正确的是()
,则下列说法正确的是()
A.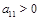 |
B.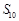 为 为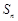 的最大值 的最大值 |
C.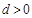 |
D.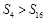 |
如图,PA垂直于圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E, F分别是点A在P B, P C上的射影,给出下列结论:
①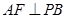 ;②
;②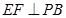 ;③
;③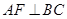 ;④
;④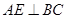 .正确命题的个数为()
.正确命题的个数为()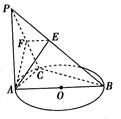
| A.1 | B.2 | C.3 | D.4 |
将函数f(x)=2sin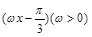 的图象向左平移
的图象向左平移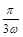 个单位,得到函数y="g" (x)的图象.若y=g(x)在[
个单位,得到函数y="g" (x)的图象.若y=g(x)在[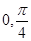 ]上为增函数,则
]上为增函数,则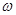 的最大值( )
的最大值( )
| A.1 | B.2 | C.3 | D.4 |
已知等比数列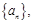 前
前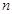 项和为
项和为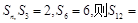 ( )
( )
| A.10 | B.20 | C.30 | D.40 |