设直线系M:
，对下列四个命题：
（1）M中所有直线均经过一
个定点
（2）存在固定区域P，M中的任一条直线都不过P
（3）对于任意整数n(n≥3),存在正n边形，其所有边均在M中的直线上
（4）M中的直线所能围成的正三角形面积相等
其中真命题的代号是 (写出所有真命题的代号)
已知椭圆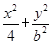
＝1(0<b<2)与y轴交于A，B两点，点F为该椭圆的一个焦点，则△ABF面积的最大值为________．
P为双曲线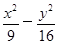
＝1的右支上一点，M、N分别是圆(x＋5)2＋y2＝4和(x－5)2＋y2＝1上的点，则PM－PN的最大值为________．
若双曲线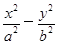
＝1(a>0，b>0)与直线y＝
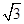x无交点，则离心率e的取值范围是________．
设椭圆C∶
＝1(a＞b＞0)恒过定点A(1,2)，则椭圆的中心到准线的距离的最小值________．
已知双曲线C与椭圆
＝1有共同的焦点F1，F2，且离心率互为倒数．若双曲线右支上一点P到右焦点F2的距离为4，则PF2的中点M到坐标原点O的距离等于________．