如图是幂函数y=xn在第一象限内的图象,已知n取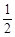 ,2,-2,-
,2,-2,-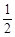 四值,则相应于曲线C1,C2,C3,C4的n依次为
四值,则相应于曲线C1,C2,C3,C4的n依次为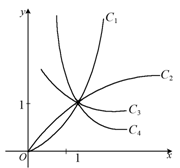
A.2,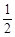 ,- ,-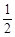 ,-2 ,-2 |
B.-2,-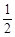 , ,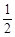 ,2 ,2 |
C.-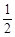 ,-2,2, ,-2,2,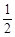 |
D.2,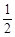 ,-2,- ,-2,-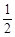 |
函数y=ax在[0,1]上的最大值与最小值之和为3,则函数y=3ax-1在[0,1]上的最大值与最小值的差是
| A.6 | B.1 | C.3 | D.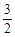 |
函数y=log2 x的反函数和y=log2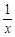 的反函数的图象关于
的反函数的图象关于
| A.x轴对称 | B.y轴对称 | C.y=x对称 | D.原点对称 |
函数f(x)=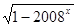 的定义域是
的定义域是
| A.(-∞,0] | B.[0,+∞) | C.(-∞,0) | D.(-∞,+∞) |
下列函数中,与函数y=x (x≥0)有相同图象的一个是
A.y=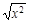 |
B.y=( )2 )2 |
C.y=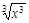 |
D.y=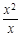 |