我校高二年级 举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰,已知选手甲答题连续两次答错的概率为
举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰,已知选手甲答题连续两次答错的概率为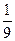 (已知甲回答每个问题的正确率相同,并且相互之间没有影响).
(已知甲回答每个问题的正确率相同,并且相互之间没有影响).
(1)求甲选手回答一个问题的正确率;
(2)求选手甲可进入决赛的概率;
(3)设选手甲在初赛中答题的个数为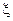 ,试写出
,试写出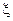 的分布列,并求
的分布列,并求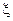 的数学期望.
的数学期望.
(本小题满分12分)已知函数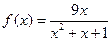 (
(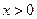 ) , (Ⅰ)试确定
) , (Ⅰ)试确定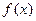 的单调区间 , 并证明你的结论 ;(Ⅱ)若
的单调区间 , 并证明你的结论 ;(Ⅱ)若 时 , 不等式
时 , 不等式 恒成立 , 求实数
恒成立 , 求实数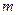 的取值范围 .
的取值范围 .
(本小题满分12分)
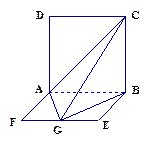 |
如图,ABCD是边长为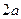 的正方形,ABEF是矩形,且二面角C
的正方形,ABEF是矩形,且二面角C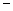 AB
AB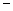 F是直二面角,
F是直二面角,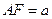 ,G是EF的中点,(Ⅰ)求证平面
,G是EF的中点,(Ⅰ)求证平面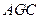 ⊥平面
⊥平面 ;
;
(Ⅱ)求GB与平面AGC所成角的正弦值.
(Ⅲ)求二面角B—AC—G的大小.
(本小题满分12分)
经统计,某大医院一个结算窗口每天排队结算的人数及相应的概率如下:
| 排队人数 |
0—5 |
6—10 |
11—15 |
16—20 |
21—25 |
25人以上 |
| 概率 |
0.1 |
0.15 |
0.25 |
0.25 |
0.2 |
0.05 |
(1)每天不超过20人排队结算的概率是多少?
(2)一周7天中,若有3天以上(含3天)出现超过15人排队结算的概率大于0.75,医院就需要增加结算窗口,请问该医院是否需要增加结算窗口?
(本小题满分12分)已知a、b、c分别是△ABC三个内角A、B、C的对边.(1)若△ABC面积为 ,c=2,A=60°,求a,b的值;(2)若acosA=bcosB,试判断△ABC的形状,证明你的结论.
,c=2,A=60°,求a,b的值;(2)若acosA=bcosB,试判断△ABC的形状,证明你的结论.
(本小题满分12分)
(理)已知Sn是正数数列{an}的前n项和,S12,S22、……、Sn2 ……,是以3为首项,以1为公差的等差数列;数列{bn}为无穷等比数列,其前四项之和为120,第二项与第四项之和为90.
(I)求an、bn;(II)从数列{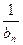 }中能否挑出唯一的无穷等比数列,使它的各项和等于
}中能否挑出唯一的无穷等比数列,使它的各项和等于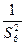 .若能的话,请写出这个数列的第一项和公比?若不能的话,请说明理由.
.若能的话,请写出这个数列的第一项和公比?若不能的话,请说明理由.