如图甲所示，两块相同的平行金属板M、N正对着放置，相距为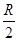
，板M、N上的小孔s1、s2与 O三点共线，s2O=R，连线s1O垂直于板M、N。以O为圆心、R为半径的圆形区域内存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场。收集屏PQ上各点到O点的距离都为2R，两端点P、Q关于连线s1O对称，屏PQ所对的圆心角θ=120°。质量为m、电荷量为e的质子连续不断地经s1进入M、N间的电场，接着通过s2进入磁场。质子重力及质子间的相互作用均不计，质子在s1处的速度看作零。
⑴若M、N间的电压UMN=+U时，求质子进入磁场时速度的大小
。
⑵若M、N间接入如图乙所示的随时间t变化的电压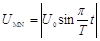
（式中
，周期T已知），且在质子通过板间电场区域的极短时间内板间电场视为恒定，则质子在哪些时刻自s1处进入板间，穿出磁场后均能打到收集屏PQ上？
⑶在上述⑵问的情形下，当M、N间的电压不同时，质子从s1处到打在收集屏PQ上经历的时间t会不同，求t的最大值。
如图所示，AB是光滑的弧形轨道，BC是距地面高为H=0.80m的光滑水平轨道。现将一小球从顶点A由静止释放，小球最后落在地面上的P点。已知A点距轨道高为h=0.45m，重力加速度g取10m/s2。求：
（1）小球通过C点时的速度大小。
（2）小球落点P与C点间的水平距离。
（3）已知小球质量为0.10kg，求小球到达P点时的动能。
如图所示，光滑斜面顶端距地面高为2.5m，斜面倾角为30º，现将一物块（可视为质点）从斜面顶端由静止释放，重力加速度g取10m/s2。求：
(1)物块在斜面上滑行时的加速度大小。
(2)物块在斜面上滑行的时间。
真空中存在着空间范围足够大的、水平向右的匀强电场。在电场中，若将一个质量为m、带正电的小球由静止释放，运动中小球速度与竖直方向夹角为37°（取sin37°＝0.6，cos37°=0.8）。现将该小球从电场中某点以初速度v0竖直向上抛出。求运动过程中
（1）小球受到的电场力的大小及方向；
（2）小球从抛出点至最高点的电势能变化量；
（3）运动过程中小球的最小动能的大小；
（4）如果抛出时的动能为4J，则小球落回到同一高度时的动能是多大？
如图，光滑水平面AB与竖直面的半圆形导轨在B点相连接，导轨半径为R，一质量为m的静止木块在A处压缩弹簧，释放后，木块获得一向右的初速度，当它经过B点进入导轨瞬间对导轨的压力是其重力的7倍，之后向上运动恰能通过轨道顶点C，不计空气阻力，试求：
(1)弹簧对木块所做的功；
(2)木块从B到C过程中克服摩擦力做的功；
(3)木块离开C点落回水平面所需的时间和落回水平面时的动能。
如图所示，电源的电动势E=220V，电阻R1=80Ω，电动机绕组的电阻R0=2Ω，电键S1始终闭合。当电键S2断开时，电阻R1的电功率是500W；当电键S2闭合时，电阻R1的电功率是320W，求：
（1）电源的内电阻；
（2）当电键S2闭合时电动机输出的机械功率。