有一个固定竖直放置的圆形轨道,半径为R,由左右两部分组成。如图所示,右半部分AEB是光滑的,左半部分BFA是粗糙的。现在最低点A给一质量为M的小球一个水平向右的初速度,使小球沿轨道恰好运动到最高点B,小球在B点又能沿BFA回到A点,到达A点时对轨道的压力为4mg。求小球由B经F回到A的过程中克服摩擦力所做的功。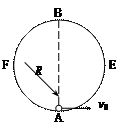

如图所示,质量为m的矩形线框MNPQ,MN边长为a,NP边长为b;MN边电阻为R1,PQ边电阻为R2,线框其余部分电阻不计。现将线框放在光滑绝缘的水平桌面上,PQ边与y轴重合。空间存在一个方向垂直桌面向下的磁场,该磁场的磁感应强度沿y轴方向均匀,沿x轴方向按规律Bx=B0(1-kx)变化,式中B0和k为已知常数且大于零。矩形线框以初速度v0从图示位置向x轴正方向平动。求: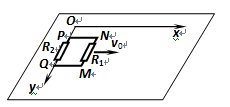
在图示位置时线框中的感应电动势以及感应电流的大小和方向;
线框所受安培力的方向和安培力的表达式;
线框的最大运动距离xm;
若R1=2R2,线框运动到
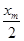 过程中,电阻R1产生的焦耳热。
过程中,电阻R1产生的焦耳热。
如图所示,在光滑绝缘水平面上B点的正上方O处固定一个质点,在水平面上的A点放另一个质点,两个质点的质量均为m,带电量均为+Q 。C为AB直线上的另一点(O、A、B、C位于同一竖直平面上),AO间的距离为L,AB和BC间的距离均为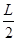 ,在空间加一个水平方向的匀强电场后A处的质点处于静止。试问:
,在空间加一个水平方向的匀强电场后A处的质点处于静止。试问:
该匀强电场的场强多大?其方向如何?
给A处的质点一个指向C点的初速度,该质点到
达B点时所受的电场力多大?若初速度大小为v0,质点到达C点时的加速度和速度分别多大?
如图所示,用内壁光滑的薄壁细圆管弯成的由半圆形APB(圆半径比细管的内径大得多)和直线BC组成的轨道固定在水平桌面上,已知APB部分的半径R=1.0 m,BC段长L=1.5m。弹射装置将一个小球(可视为质点)以v0=5m/s的水平初速度从A点弹入轨道,小球从C点离开轨道随即水平抛出,落地点D离开C的水平距离s=2m,不计空气阻力,g取10m/s2。求: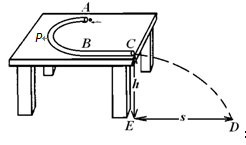
小球在半圆轨道上运动时的角速度ω和加速度a的大小;
小球从A点运动到C点的时间t;
桌子的高度h。
如图所示,质量为m,电量为q的带电粒子以初速v0进入场强为E的匀强电场中,电场长度为L,电容器极板中央到光屏的距离也是L.已知带电粒子打到光屏的P点,求偏移量OP的大小.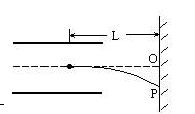
如图所示,均匀带电圆环所带电电荷量为Q,半径为R,圆心为O,P为垂直于圆环平面的对称轴上的一点,OP=L,试求P点的电场强度.