一个质量m=0.1kg的正方形金属框总电阻R=0.5Ω，金属框放在表面绝缘且光滑的斜面顶端（金属框上边与AA′重合），自静止开始沿斜面下滑，下滑过程中穿过一
段边界与斜面底边BB′平行、宽度为d的匀强磁场后滑至斜面底端（金属框下边与BB′重合），设金属框在下滑过程中的速度为v，与此对应的位移为s，那么v2—s图象如图所示，已知匀强磁场方向垂直斜面向上.试问：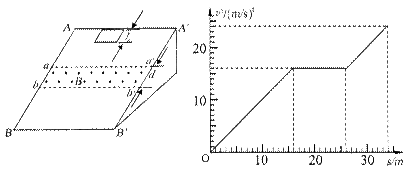
（1）根据v2—s图象所提供的信息，计算出斜面倾角θ和匀强磁场宽度d.
（2）匀强磁场的磁感强度多大？金属框从斜面顶端滑至底端所需的时间为多少？
（3）现用平行斜面沿斜面向上的恒力F作用在金属框上，使金属框从斜面底端BB′（金属框下边与BB′重合）由静止开始沿斜面向上运动，匀速通过磁场区域后到达斜面顶端（金属框上边与AA′重合）.试计算恒力F做功的最小值.
如图15所示为一真空示波管，电子从灯丝K发出（初速度不计），经灯丝与A板间的加速电压U1加速，从A板中心孔沿中心线KO射出，然后进入两块平行金属板M、N形成的偏转电场中（偏转电场可视为匀强电场），电子进入M、N间电场时的速度与电场方向垂直，电子经过电场后打在荧光屏上的P点。已知加速电压为U1，M、N两板间的电压为U2，两板间的距离为d，板长为L1，板右端到荧光屏的距离为L2，电子的质量为m，电荷量为e。求：
（1）电子穿过A板时的速度大小；
（2）电子从偏转电场射出时的侧移量；
（3）P点到O点的距离。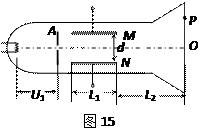
如图13-6-7所示，质量为0.2Kg的物体带电量为+4×10-4C，从半径为0.3m的光滑的1/4圆弧的绝缘滑轨上端静止下滑到底端，然后继续沿水平面滑动。物体与水平面间的滑动摩擦系数为0.4，整个装置处于E=103N/C的匀强电场中，求下列两种情况下物体在水平面上滑行的最大距离：(1)E水平向左；(2)E竖直向下。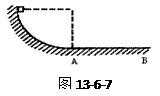
如图所示，质量为
，带电量为
的小球，在P点具有沿PQ方向的初速度
，为使小球能沿PQ方向运动，施加一垂直于PQ沿斜向左上方的匀强电场，求：（1）所加电场的电场强度为多大？（2）小球经多长时间回到P点？
如图所示，倾角为θ的光滑绝缘斜面固定在水平面上，整个空间存在垂直斜面向下的匀强磁场，磁感应强度为B，有一长为L质量为m的通电直导线垂直纸面水平放置在斜面上恰能保持静止，试判断通电直导线的电流方向并求出电流的大小。（已知重力加速度为g）
一纯电阻闭合电路,电源电动势为4.5V，内阻为0.5Ω，外电路的电阻为4.0Ω，则：
（1）路端电压是多大？
（2）如果在外电路上并联一个6.0Ω的电阻，路端电压是多大？
（3）如果（2）中的6.0Ω电阻不是并联，而是串联在外电路中，路端电压又是多大？