在做“用油膜法估测分子大小”的实验中，所用油酸酒精溶液的浓度为每104mL溶液中有纯油酸6mL，用注射器测得1mL上述溶液有75滴，把1滴该溶液滴入盛水的浅盘里，待水面稳定后，将玻璃板放在浅盘上，用笔在玻璃板上描出
油酸的轮廓，再把玻璃板放在坐标纸上，其形状和尺寸如图所示，坐标中正方形方格的边长为2cm，试求
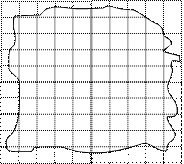
（1）油酸膜的面积是多少cm2；
（2）每滴油酸酒精溶液中含有纯油酸的体积；
（3）按以上实验数据估测出油酸分子的直径。
跳伞运动员从跳伞塔上跳下，当降落伞打开后，伞和运动员所受的空气阻力大小跟下落速度的平方成正比，即f=kv2，已知比例系数k =20N
s2/m2，运动员和伞的总质量m=72kg．设跳伞塔足够高，且运动员跳离塔后即打开伞，取g=10m/s2．
（1）求下落速度达到v=3m/s时，跳伞运动员的加速度大小；
（2）求跳伞运动员最终下落的速度；
（3）若跳伞塔高h=200m，跳伞运动员在着地前已经做匀速运动，求从开始跳下到即将触地的过程中，伞和运动员损失的机械能．
如图所示,在质量为
的电动机上，装有质量为
的偏心轮，偏心轮的重心
距转轴的距离为
.当偏心轮重心在转轴
正上方时，电动机对地面的压力刚好为零.求电动机转动的角速度
.
某探究小组设计了一个质谱仪，其原理如图所示.一束电量均为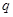
，质量不同的带负电的粒子，经过电场加速后进入一速度选择器，从
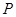点进入一等腰直角三角形的有界磁场中，又从斜边射出.速度选择器中垂直纸面向里的匀强磁场的磁感应强度为
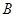，竖直向下的匀强电场强度为
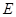，有界磁场的磁感应强度为
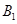，直角边长为
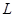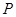，为斜边的中点，
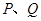两点相距为
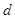.求：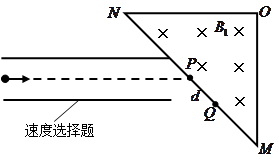
（1）带电粒子进入有界磁场的速度大小.
（2）带电粒子质量应满足的条件.
（3）打在斜边上Q点的带电粒子在磁场中运动的时间.
两个质量分别为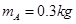
、
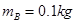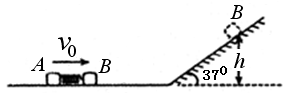
的小滑块A、B和一根轻质短弹簧，弹簧的一端与小滑块A粘连，另一端与小滑块B接触而不粘连.现使小滑块A和B之间夹着被压缩的轻质弹簧，处于锁定状态，一起以速度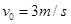
在水平面上做匀速直线运动，如题8图所示.一段时间后，突然解除锁定（解除锁定没有机械能损失），两滑块仍沿水平面做直线运动，两滑块在水平面分离后，小滑块B冲上斜面的高度为
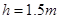.斜面倾角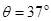
，小滑块与斜面间的动摩擦因数为
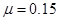，水平面与斜面圆滑连接.重力加速度
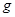取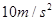
.求：（提示：
，
）
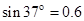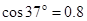（1）A、B滑块分离时，B滑块的速度大小.
（2）解除锁定前弹簧的弹性势能.
一匀强电场，场强方向水平向左，如题7图所示.一个质量为
的带正电的小球，从
点出发，初速度的大小为
，在静电力与重力的作用下，恰能沿与场强的反方向成
角的直线运动.求：
（1）小球运动的加速度大小.
（2）小球从点运动到最高点的过程中电势能的变化.