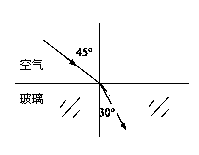地球的第一宇宙速度 约为
约为 ,地球表面附近的重力加速度约为10m/s2,由这两个量估算近地人造卫星的环绕周期T约为多少?
,地球表面附近的重力加速度约为10m/s2,由这两个量估算近地人造卫星的环绕周期T约为多少?
(14分)如图所示,水平方向有界匀强磁场的高度h=1m、磁感应强度B=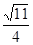 T。竖直放置的“日”字型闭合导体线框ABFE,宽L=1m,质量m=0.25kg,AC、CE的长度都大于h,AB边的电阻RAB=1Ω、CD边的电阻RCD=2Ω、EF边的电阻REF=3Ω,其余电阻不计。线框由静止下落,AB边进入磁场时恰能匀速运动,不计空气阻力,g取10m/s2。求:
T。竖直放置的“日”字型闭合导体线框ABFE,宽L=1m,质量m=0.25kg,AC、CE的长度都大于h,AB边的电阻RAB=1Ω、CD边的电阻RCD=2Ω、EF边的电阻REF=3Ω,其余电阻不计。线框由静止下落,AB边进入磁场时恰能匀速运动,不计空气阻力,g取10m/s2。求: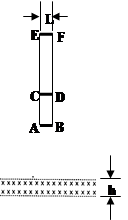
(1)开始下落时,线框AB边离磁场上边界的高度h1为多少?
(2)若线框CD边刚进入磁场时也做匀速运动,AB边与CD边的距离h2为多少?
(3)在满足(1)(2)前提下,若线框EF边刚进磁场时也做匀速运动,则从开始下落到EF边离开磁场过程中,线框中产生的焦耳热Q为多少?
质量为m=1.0kg、带电量q=+2.5×10-4C的小滑块(可视为质点)放在质量为M=2.0kg的绝缘长木板的左端,木板放在光滑水平面上,滑块与木板之间的动摩擦因数为μ=0.2,木板长L=1.5m,开始时两者都处于静止状态,所在空间加有一个方向竖直向下强度为E=4.0×104N/C的匀强电场,如图所示.取g=10m/s2,试求:
(1)用水平力F0拉小滑块,要使小滑块与木板以相同的速度一起运动,力F0应满足什么条件?
(2)用水平恒力F拉小滑块向木板的右端运动,在1.0s末使滑块从木板右端滑出,力F应为多大?
(3)按第(2)问的力F作用,在小滑块刚刚从木板右端滑出时,系统的内能增加了多少?(设m与M之间最大静摩擦力与它们之间的滑动摩擦力大小相等,滑块在运动中带电量不变)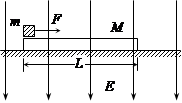
(8分)如图所示,在一矩形区域内,不加磁场时,不计重力的带电粒子以某一初速度垂直左边界射入,穿过此区域的时间为t.若加上磁感应强度为B、垂直纸面向外的匀强磁场,带电粒子仍以原来的初速度入射,粒子飞出磁场时偏离原方向60°,利用以上数据求:带电粒子的比荷及带电粒子在磁场中运动的周期
一静止的铀核(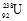 )发生α衰变转变成钍核(Th),已知放出的α粒子速度为v0=2.0×106m/s.假设铀核发生衰变时,释放的能量全部转化为α粒子和钍核的动能.试写出铀核衰变的核反应方程并求出钍核(Th)的反冲速度。(结果保留两位有效数字)
)发生α衰变转变成钍核(Th),已知放出的α粒子速度为v0=2.0×106m/s.假设铀核发生衰变时,释放的能量全部转化为α粒子和钍核的动能.试写出铀核衰变的核反应方程并求出钍核(Th)的反冲速度。(结果保留两位有效数字)
一束单色光由空气入射到某平板玻璃表面,入射光及折射光光路如图所示。求该单色光在玻璃中的临界角。