如图甲所示,空间存在竖直向上磁感应强度B="1" T的匀强磁场,ab、cd是相互平行间距L="1" m的长直导轨,它们处在同一水平面内,左边通过金属杆ac相连,质量m="1" kg的导体棒MN水平放置在导轨上,已知MN与ac的总电阻R="0.2" Ω,其他电阻不计.导体棒MN通过不可伸长细线经光滑定滑轮与质量也为m的重物相连,现将重物由如图所示的静止状态释放后与导体棒MN一起运动,并始终保持导体棒与导轨接触良好.已知导体棒与导轨间的动摩擦因数为μ=0.5,其他摩擦不计,导轨足够长,重物离地面足够高,重力加速度g取10 m/s2.
(1)请定性说明:导体棒MN在达到匀速运动前,速度和加速度是如何变化的;到达匀速运动时MN受到的哪些力合力为零,并在图乙中定性画出棒从静止至匀速的过程中所受的安培力大小随时间变化的图象(不需说明理由及计算达到匀速的时间).
(2)若已知重物下降高度h="2" m时,导体棒恰好开始做匀速运动,在此过程中ac边产生的焦耳热Q="3" J,求导体棒MN的电阻值r.
如图所示光滑平行金属轨道abcd,轨道的水平部分bcd处于竖直向上的匀强磁场中,bc部分平行导轨宽度是cd部分的2倍,轨道足够长。将质量相同的金属棒P和Q分别置于轨道的ab段和cd段。P棒位于距水平轨道高为h的地方,放开P棒,使其自由下滑,求P棒和Q棒的最终速度。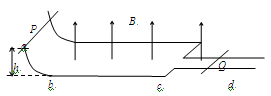
如图所示,长为6m的导体AB在磁感强度B=0.1T的匀强磁场中,以AB上的一点O为轴,沿着顺时针方向旋转。角速度ω=5rad/s,O点距A端为2m,求AB的电势差。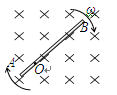
在如图所示的水平导轨上(摩擦、电阻忽略不计),有竖直向下的匀强磁场,磁感强度B,导轨左端的间距为L1=4l0,右端间距为l2=l0。今在导轨上放置AC、DE两根导体棒,质量分别为m1=2m0,m2=m0,电阻R1=4R0,R2=R0。若AC棒以初速度v0向右运动,求AC棒运动的过程中产生的总焦耳热QAC,以及通过它们的总电量q。
共有100匝的矩形线圈,在磁感强度为0.1T的匀强磁场中以角速度ω=10rad/s绕线圈的中心轴旋转。已知线圈的长边a=20cm,短边b=10cm,线圈总电阻为2Ω。求
(1)线圈平面转到什么位置时,线圈受到的电磁力矩最大?最大力矩有多大?
(2)线圈平面转到与磁场方向夹角60°时,线圈受到的电磁力矩。
如图所示,在磁感强度B= 2T的匀强磁场中,有一个半径r=0.5m的金属圆环。圆环所在的平面与磁感线垂直。OA是一个金属棒,它沿着顺时针方向以20rad/s的角速度绕圆心O匀速转动。A端始终与圆环相接触OA棒的电阻R=0.1Ω,图中定值电阻R1=100Ω,R2=4.9Ω,电容器的电容C=100pF。圆环和连接导线的电阻忽略不计,求: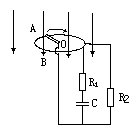
(1)电容器的带电量。哪个极板带正电。
(2)电路中消耗的电功率是多少?