如图所示,在一次消防演习中,消防员练习使用挂钩从高空沿滑杆由静止滑下,滑杆由AO、OB两段直杆通过光滑转轴连接在O处,可将消防员和挂钩均理想化为质点,且通过O点的瞬间没有机械能的损失.AO长为 =5m,OB长为
=5m,OB长为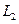 =10m.两堵竖直墙的间距
=10m.两堵竖直墙的间距 =11m.滑杆A端用铰链固定在墙上,可自由转动.B端用铰链固定在另一侧墙上.为了安全,消防员到达对面墙的速度大小不能超过6m/s,挂钩与两段滑杆间动摩擦因数均为
=11m.滑杆A端用铰链固定在墙上,可自由转动.B端用铰链固定在另一侧墙上.为了安全,消防员到达对面墙的速度大小不能超过6m/s,挂钩与两段滑杆间动摩擦因数均为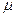 =0.8(
=0.8( =10m/s2,sin37°=0.6,cos37°=0.8)
=10m/s2,sin37°=0.6,cos37°=0.8)
(1)若测得消防员下滑时,OB段与水平方向间的夹角始终为37°,求消防员在两滑杆上运动时加 速度的大小及方向;
速度的大小及方向;
(2)若B端在竖直墙上的位置可以改变,求滑杆端点A、B间 的最大竖直距离.
如图所示,一定质量的气体温度保持不变,最初,U形管两臂中的水银相齐,烧瓶中气体体积为800mL;现用注射器向烧瓶中注入200mL水,稳定后两臂中水银面的高度差为25cm,不计U形管中气体的体积。求:
①大气压强是多少cmHg?
②当U形管两边水银面的高度差为45cm时,烧瓶内气体的体积是多少?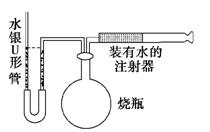
如图,离子源A产生的初速为零、带电量均为e、质量不同的正离子被电压为U 0的加速电场加速后匀速通过准直管,垂直射入匀强偏转电场,偏转后通过极板HM上的小孔S离开电场,经过一段匀速直线运动,垂直于边界MN进入磁感应强度为B的匀强磁场。已知HO=d,HS=2d,  =90°。
=90°。
(忽略粒子所受重力和一切阻力)
(1)求偏转电场场强E 0的大小以及HM与MN的夹角 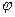 ;
;
(2)求质量为m的离子在磁场中做圆周运动的半径;
(3)若质量为4m的离子垂直打在NQ的中点  处,质量为16m的离子打在
处,质量为16m的离子打在  处。求
处。求  和
和  之间的距离。
之间的距离。 
如图所示,在水平匀速运动的传送带的左端(P点),轻放一质量为m=1kg的物块,物块随传送带运动到A点后抛出,物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑圆弧轨道下滑。B、D为圆弧的两端点,其连线水平。已知圆弧半径R=1.0m,圆弧对应的圆心角θ=106º,轨道最低点为C,A点距水平面的高度h=0.80m,AB的水平距离为1.2m。(g=10m/s2,sin53º=0.8,cos53º=0.6)求:
⑴物块离开A点时水平初速度的大小;
⑵物块经过C点时对轨道压力的大小;
⑶设物块与传送带间的动摩擦因数为0.3,传送带的速
度为5m/s,求PA间的距离。
如图所示,在车厢中,一小球被a、b两根轻质细绳拴住,其中a绳与竖直方向成α角,绳b成水平状态,已知小球的质量为m,求:
(1)车厢静止时,细绳a和b所受到的拉力。
(2)当车厢以一定的加速运动时,a绳与竖直方向的夹角不变,而b绳受到的拉力变为零,求此时车厢的加速度的大小和方向。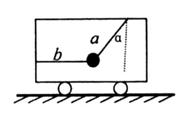
气球以10m/s的速度匀速上升,在离地面75m高处从气球上掉落一个物体,结果气球便以加速度α=0.1m/s2向上做匀加速直线运动,不计物体在下落过程中受到的空气阻力,问物体落到地面时气球离地的高度为多少?g=10m/s2.