已知:如图,在等边三角形ABC中,M、N分别是AB、AC的中点,D是MN上任意一点,CD、BD的延长线分别与AB、AC交于F、E,若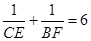 ,则等边三角形ABC的边长为
,则等边三角形ABC的边长为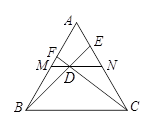
A. 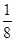 B.
B. 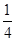 C.
C. 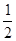 D.1
D.1
如图,在□ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为().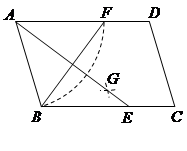
| A.4 | B.6 | C.8 | D.10 |
小王参加某企业招聘测试,他的笔试,面试、技能操作得分分别为85分,80分,90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是().
| A.255分 | B.84分 | C.84.5分 | D.86分 |
不等式组 的解集在数轴上表示为().
的解集在数轴上表示为().
|
|
|
|
|
|
|
|
|
|
|
|

如图,直线a,b被直线e,d所截,若∠1=∠2,∠3=125°,则∠4的度数为().
| A.55° | B.60° | C.70° | D.75° |
据统计,2014年我国高新技术产品出口总额达40570亿元,将数据40570亿用科学记数法表示为().
| A.4.0570×109 | B.0.40570×1010 | C.40.570×1011 | D.4.0570×1012HHH |