人造卫星是由运载火箭点火发射后送入 其 运行轨道的,其发射后的飞行过程大致可分为:垂直加速阶段、惯性飞行阶段和进入轨道阶段,如图所示。设地球表面g="10" m/s2,地球的半径R="6.4×103" km
(1)设某次发射过程中,有一在地球表面重 为 40 N的物体,放置在该卫星中。在卫星垂直加速上升的过程中,且a="5" m/s2时物体与卫星中的支持面的相互作用30 N,则卫星此时距地面的高度为 km。
(2)当卫星进入离地高为地球半径3倍的圆形轨道运动时,它运行的速度为 km/s
两根相距为L的足够长的金属直角导轨如图所示放置,它们各有一边在同一水平面内,另一边垂直于水平面.质量均为m的金属细杆ab、cd与导轨垂直接触形成闭合回路,杆与水平和竖直导轨之间有相同的动摩擦因数μ,导轨电阻不计,回路总电阻为2R,整个装置处于磁感应强度大小为B、方向竖直向上的匀强磁场中.当ab杆在平行于水平导轨的拉力作用下沿导轨向右匀速运动时,cd杆也正好以某一速度向下做匀速运动,设运动过程中金属细杆ab、cd与导轨接触良好,重力加速度为g,求:
(1)ab杆匀速运动的速度v1;
(2)ab杆所受拉力F;
(3)ab杆以v1匀速运动时,cd杆以v2(v2已知)匀速运动,则在cd杆向下运动 过程中,整个回路中产生的焦耳热.
过程中,整个回路中产生的焦耳热.
如图(a)所示,木板OA可绕轴O在竖直平面内转动,某研究小组利用此装置探索物块在方向始终平行于斜面、大小为F=8N的力作用下加速度与斜面倾角的关系。已知物块的质量m=1kg,通过DIS实验,得到如图(b)所示的加速度与斜面倾角的关系图线。若物块与木板间的动摩擦因数为0.2,假定物块与木板间的最大静摩擦力始终等于滑动摩擦力,g取10m/s2。试问: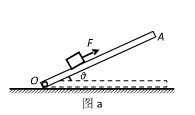
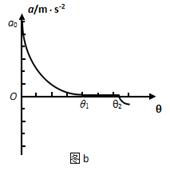
(1)图(b)中图线与纵坐标交点ao多大?
(2)图(b)中图线与θ轴交点坐标分别为θ1和θ2,木板处于该两个角度时的摩擦力指向何方?说明在斜面倾角处于θ1和θ2之间时物块的运动状态。
(3)θ1为多大?
(4)如果木板长L=2m,倾角为37°,物块在F的作用下由O点开始运动,为保证物块不冲出木板顶端,力F最多作用多长时间?(取sin37°=0.6,cos37°=0.8)
(19分)如图所示,带正电的绝缘小滑块A,被长R=0.4m的绝缘细绳竖直悬挂,悬点O距水平地面的高度为3R;小滑块B不带电.位于O点正下方的地面上。长L=2R的绝缘水平传送带上表面距地面的高度h=2R,其左端与O点在同一竖直线上,右端的右侧空间有方向竖直向下的匀强电场。在O点与传送带之间有位置可调的固定钉子(图中未画出),当把A拉到水平位置由静止释放后,因钉子阻挡,细绳总会断裂,使得A能滑上传送带继续运动,若传送带逆时针匀速转动,A刚好能运动到传送带的右端。已知绝缘细绳能承受的最大拉力是A重力的5倍,A所受电场力大小与重力相等,重力加速度g=10m/s2,A.B均可视为质点,皮带传动轮半径很小,A不会因绳断裂而损失能量、也不会因摩擦而损失电荷量。试求:
(1)钉子距O点的距离的范围。
(2)若传送带以速度v0=5m/s顺时针匀速转动,在A刚滑到传送带上时,B从静止开始向右做匀加速直线运动,当A刚落地时,B恰与A相碰。试求B做匀加速运动的加速度大小(结果可用根式表示)
(17分)如图甲所示,带斜面的足够长木板P,质量M=3kg.静止在水平地面上,其右侧靠竖直墙壁,倾斜面BC与水平面AB的夹角 、两者平滑对接。t=Os时,质量m=1kg、可视为质点的滑块Q从顶点C由静止开始下滑,图乙所示为Q在O~6s内的速率
、两者平滑对接。t=Os时,质量m=1kg、可视为质点的滑块Q从顶点C由静止开始下滑,图乙所示为Q在O~6s内的速率 随时间t变化的部分图线。已知P与Q间的动摩擦因数是P与地面间的动摩擦因数的5倍,sin370=0.6,cos370=O.8,g取10m/s2。求:
随时间t变化的部分图线。已知P与Q间的动摩擦因数是P与地面间的动摩擦因数的5倍,sin370=0.6,cos370=O.8,g取10m/s2。求:
(1)木板P与地面间的动摩擦因数。
(2)t=8s时,木板P与滑块Q的速度大小。
(3)O~8s内,滑块Q与木板P之间因摩擦而产生的热量。
(15分)我国拥有航空母舰后,舰载机的起飞与降落等问题受到了广泛关注。2012年11月23日,舰载机歼一15首降“辽宁舰”获得成功,随后舰载机又通过滑跃式起飞成功。某兴趣小组通过查阅资料对舰载机滑跃起飞过程进行了如下的简化模拟:假设起飞时“航母”静止,飞机质量视为不变并可看成质点。“航母”起飞跑道由图示的两段轨道组成(二者平滑连接,不计拐角处的长度),其水平轨道长AB=L,水平轨道与斜面轨道末端C的高度差为h。一架歼一15飞机的总质量为m.在C端的起飞速度至少为 。若某次起飞训练中,歼一15从A点由静止启动,飞机发动机的推力大小恒为0.6mg,方向与速度方向相同,飞机受到空气和轨道平均阻力的合力大小恒为0.1mg。重力加速度为g。求:
。若某次起飞训练中,歼一15从A点由静止启动,飞机发动机的推力大小恒为0.6mg,方向与速度方向相同,飞机受到空气和轨道平均阻力的合力大小恒为0.1mg。重力加速度为g。求:
(1)飞机在水平轨道AB上运动的时间。
(2)在水平轨道末端B,发动机的推力功率。
(3)要保证飞机正常起飞,斜面轨道的长度满足的条件。(结果用m、g、L、h、 表示)
表示)