在一次数学考试中, 第14题和第15题为选做题。规定每位考生必须且只须在其中选做一题. 设4名考生选做这两题的可能性均为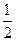 .
.
(Ⅰ)其中甲、乙2名学生选做同一道题的概率;
(Ⅱ)设这4名考生中选做第15题的学生数为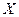 个,求
个,求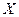 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠DAB=60°.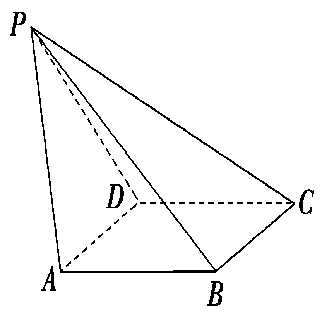
(1)证明:∠PBC=90°;
(2)若PB=3,求直线AB与平面PBC所成角的正弦值.
(本小题满分12分)如图:在三棱锥 中,已知点
中,已知点 、
、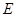 、
、 分别为棱
分别为棱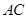 、
、 、
、 的中点.
的中点.
(1)求证: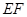 ∥平面
∥平面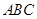 ;
;
(2)若 ,
,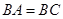 ,求证:平面
,求证:平面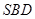 ⊥平面
⊥平面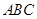 .
.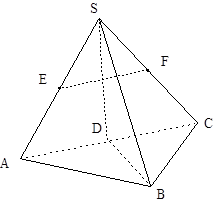
(本小题满分12分)如图,已知平面 ∩平面
∩平面 =AB,PQ⊥
=AB,PQ⊥ 于Q,PC⊥
于Q,PC⊥ 于C,CD⊥
于C,CD⊥ 于D.
于D.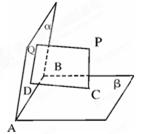
(1)求证:P、C、D、Q四点共面;
(2)求证:QD⊥AB.
(本小题满分12分) 求满足下列条件的椭圆的标准方程.
(1)焦点在坐标轴上,且经过两点 ;
;
(2)经过点(2,-3)且与椭圆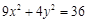 具有共同的焦点.
具有共同的焦点.
(本小题满分14分)某公司生产的新产品的成本是2元/件,售价是3元/件,
年销售量为10万件,为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是 (万元)时,产品的销售量将是原销售量的
(万元)时,产品的销售量将是原销售量的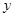 倍,且
倍,且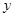 是
是 的二次函数,它们的关系如下表:
的二次函数,它们的关系如下表:
 |
··· |
1 |
2 |
··· |
5 |
··· |
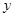 |
··· |
1.5 |
1.8 |
··· |
1.5 |
··· |
(2)求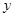 与
与 的函数关系式;
的函数关系式;
(3)如果利润=销售总额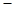 成本费
成本费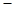 广告费,试写出年利润S(万元)与广告费
广告费,试写出年利润S(万元)与广告费 (万元)的函数关系式;并求出当广告费
(万元)的函数关系式;并求出当广告费 为多少万元时,年利润S最大.
为多少万元时,年利润S最大.