如图1,在△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长.
小萍同学灵活运用轴对称知识,将图形进行翻折变换如图1.她分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,得到四边形AEGF是正方形.设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值.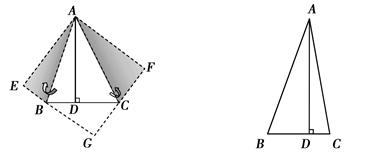
(1)请你帮小萍求出x的值.
(2) 参考小萍的思路,探究并解答新问题:
如图2,在△ABC中,∠BAC=30°,AD⊥BC于D,AD=4.请你按照小萍的方法画图,得到四边形AEGF,求△BGC的周长.(画图所用字母与图1中的字母对应)
已知:如图8,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
(1)求证:∠BAC=∠CAD
某学校九年级的学生去旅游,在风景区看到一棵古松,不知这棵古松有多高,下面是他们的一段对话:
甲:我站在此处看树顶仰角为45°。
乙:我站在此处看树顶仰角为30°。
甲:我们的身高都是1.5m。
乙:我们相距20m。
请你根据两位同学的对话,参考图7计算这棵古松的高度。(参考数据 ≈1.414,
≈1.414, ≈1
≈1 .732,结果保留两位小数)。
.732,结果保留两位小数)。 图7
图7
学校在艺术周上,要求学生制作一个 精美的轴对称图形,请你用所给出的几何图形:○○△
精美的轴对称图形,请你用所给出的几何图形:○○△ △(两个圆,两个等边三角形,两条线段)为构件,构思一个独特,有意义的轴对称图形,并写上一句简要的解说词。
△(两个圆,两个等边三角形,两条线段)为构件,构思一个独特,有意义的轴对称图形,并写上一句简要的解说词。
请你先化简分式
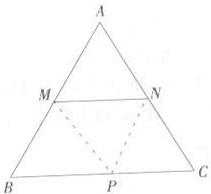
在等腰△ABC中,AB=AC=5,BC=6.动点M、N分别在两腰AB、AC上(M不与A、B重合,N不与A、C重合),且MN∥BC.将△AMN沿MN所在的直线折叠,使点A的对应点为P.
(1)当MN为何值时,点P恰好落在BC上?
(2)当MN=x,△MNP与等腰△ABC重叠部分的面积为y,试写出y与x的函数关系式.当x为何值时,y的值最大,最大值是多少?