如图所示，竖
直平面内有一半径为r、内阻为R1、粗细均匀的光滑半圆形金属环，在M、N处与相距为2r、电阻不计的平行光滑金属轨道ME、NF相接，EF之间接有电阻R2，已知R1＝12R，R2＝4R。在MN上方及CD下方有水平方向的匀强磁场I和II，磁感应强度大小均为B。现有质量为m、电阻不计的导体棒ab，从半圆环的最高点A处由静止下落，在下落过程中导体棒始终保持水平，与半圆形金属环及轨道接触良好，设平行轨道足够长。已知导体棒ab下落r/2时的速度大小为v1，下落到MN处的速度大小为v2。
（1）求导体棒ab从A下落r/2时的加速度大小。
（2）若导体棒ab进入磁场II后棒中电流大小始终不
变，求磁场I和I
I之间的距离h和R2上的电功率P2。 
一列长L=200m的列车以v0＝72 km/h的正常速度匀速运行，当它从开上长L0＝1000 m的某大桥到全部车厢通过大桥，列车必须以v＝54 km/h的限制速度匀速运行．已知列车在上桥前减速过程中的加速度大小与过桥后加速恢复正常速度过程中的加速度大小相等，均为a＝0.5 m/s2， 且列车加速和减速过程均可视为匀变速直线运动。求列车因为过桥而延误的时间t．
如图所示，A、B两小球带等量同号电荷，A固定在竖直放置的L=10cm长的绝缘支杆上，B受A的斥力作用静止于光滑的绝缘斜面上与A等高处，斜面倾角为
=300，B的质量为m=360g。
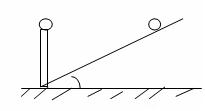
求：（1）B球对斜面的压力大小
（2）B 球带的电荷量大小（g取10m/s2，结果保留两位有效数字）。
如图所示，水平桌面上有一轻弹簧，左端固定在A点，自然状态时其右端位于B点。水平桌面右侧有一竖直放置的光滑轨道MNP，其形状为半径R=0.8m的圆环剪去了左上角135°的圆弧，MN为其竖直直径，P点到桌面的竖直距离也是R、水平距离是2R。用质量m=0.4kg的物块将弹簧缓慢压缩到C点，释放后物块过B点后其位移与时间的关系为
，物块飞离桌边缘D点后由P点沿切线落入圆轨道。g=10m/s2，求：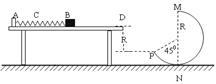
（1）BD间的水平距离；
（2）滑块运动到N处时对轨道的压力；
（3）判断m能否沿圆轨道到达M点（说明理由）
如图所示，质量m=lkg的物块从h=0.8m高处沿光滑斜面滑下，到达底部时通过光滑圆弧BC滑至水平传送带CE上，CE长L=3m．D是CE之间的一点，距离C点2m。传送带在皮带轮带动下，以v=4m/s的速度逆时针传动，物块与传送带间动摩擦因数μ=0.3,求：
（1）物块第一次通过C、D两点时的速度大小各为多少?
（2）物块从出发到第二次经过D点的过程中，皮带对物块做多少功?
（3）物块从出发到第二次经过D点的过程中，因摩擦产生的热量是多少?
如图所示为足够长斜面，其倾角为θ＝37°，一质量m＝10kg物体，在斜面底部受到一个沿斜面向上的F＝100 N的力作用由静止开始运动，物体在2s内位移为4m，2s末撤去力F，(sin 37°＝0.6，cos 37°＝0.8，g＝10m/s2)求：
(1)物体与斜面间的动摩擦因数μ；
(2)从撤掉力F开始1.5 s末物体的速度v；
(3) 什么时候物体经过离斜面底部4.5m处。