如图1,平面直角坐标系 xOy中,A
xOy中,A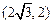 ,B
,B .将△OAB绕点O顺时针旋转a角(0°<a<90°)得到△OCD(O,A,B的对应点分别为O,C,D),将△OAB沿
.将△OAB绕点O顺时针旋转a角(0°<a<90°)得到△OCD(O,A,B的对应点分别为O,C,D),将△OAB沿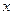 轴负方向平移m个单位得到△EFG(m>0,O,A,B的
轴负方向平移m个单位得到△EFG(m>0,O,A,B的 对应点分别为E,F,G),a,m的值恰使点C,D,F落在同一反比例函数
对应点分别为E,F,G),a,m的值恰使点C,D,F落在同一反比例函数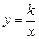 (k≠0)的图象上.
(k≠0)的图象上.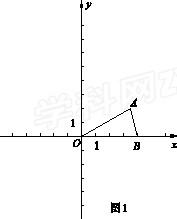
(1)∠AOB=" " °,a=" " °;
(2)求经过点A,B,F的抛物线的解析式;
(3)若(2)中抛物线的顶点为M,抛物线与直线EF的另一个交点为H,抛物线上的点P满足以P,M,F,A为顶点的四边形的面积与四边形MFAH的面积相等(点P不与点H重合),请直接写出满足条件的点P的个数,并求位于直线EF上方的点P 的坐标.
的坐标.
奥体中心为满足暑期学生对运动的需求,欲开设球类课程,该中心随机抽取部分学生进行问卷调查,被调查学生须从“羽毛球”、“篮球”、“足球”、“排球”、“乒乓球”中选择自己最喜欢的一项.根据调查结果绘制了不完整的条形统计图和扇形统计图,请根据图中信息,解答下列问题:
(1)此次共调查了多少名学生?
(2)将条形统计图补充完整;
(3)我们把“羽毛球”“篮球”,“足球”、“排球”、“乒乓球”分别用 , , , , 表示.小明和小亮分别从这些项目中任选一项进行训练,利用树状图或表格求出他俩选择不同项目的概率.

先化简,再求值: ,其中 , .
如图,抛物线 与 轴交于点 和点 ,与 轴交于点 ,顶点为 ,连接 , , 与抛物线的对称轴 交于点 .
(1)求抛物线的表达式;
(2)点 是第一象限内抛物线上的动点,连接 , ,当 时,求点 的坐标;
(3)点 是对称轴 右侧抛物线上的动点,在射线 上是否存在点 ,使得以点 , , 为顶点的三角形与 相似?若存在,求点 的坐标;若不存在,请说明理由.

如图1,在 中, , ,点 , 分别在边 , 上,且 ,连接 .现将 绕点 顺时针方向旋转,旋转角为 ,如图2,连接 , , .
(1)当 时,求证: ;
(2)如图3,当 时,延长 交 于点 ,求证: 垂直平分 ;
(3)在旋转过程中,求 的面积的最大值,并写出此时旋转角 的度数.

因疫情防控需要,消毒用品需求量增加.某药店新进一批桶装消毒液,每桶进价50元,每天销售量 (桶 与销售单价 (元 之间满足一次函数关系,其图象如图所示.
(1)求 与 之间的函数表达式;
(2)每桶消毒液的销售价定为多少元时,药店每天获得的利润最大,最大利润是多少元?(利润 销售价 进价)
