已知P是直线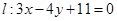 上的动点,PA、PB是圆
上的动点,PA、PB是圆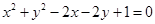 的两条切线,C是圆心,那么四边形PACB面积的最小值是()
的两条切线,C是圆心,那么四边形PACB面积的最小值是()
A.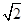 B.2
B.2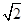 C.
C.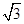 D.2
D.2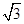
抛掷一枚骰子,当它每次落地时,向上的点数称为该次抛掷的点数,可随机出现1到6点中的任一个结果,连续抛掷三次,将第一次,第二次,第三次抛掷的点数分别记为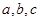 ,求长度为
,求长度为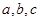 的三条线段能构成等腰三角形的概率为()
的三条线段能构成等腰三角形的概率为()
A.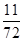 |
B.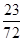 |
C.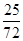 |
D.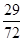 |
如下图程序框图所示,最终输出的结果为()
A.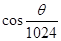 |
B.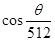 |
C. |
D.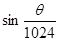 |
 的展开式中各项系数的和为2,则该展开式中常数项为()
的展开式中各项系数的和为2,则该展开式中常数项为()
| A.-20 | B.—10 | C.10 | D.20 |
为迎接新年,帮助离退休教师打扫卫生,校团委招募了 名志愿者,他们的编号分别是
名志愿者,他们的编号分别是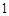 号,
号, 号,
号,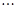 ,
,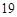 号,
号, 号.若要从这些志愿者中任意挑选
号.若要从这些志愿者中任意挑选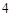 人再按编号大小分成两组去做一些准备工作,其中两个编号较小的人在一组,另两个编号较大的人在另一组,那么确保
人再按编号大小分成两组去做一些准备工作,其中两个编号较小的人在一组,另两个编号较大的人在另一组,那么确保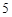 号与
号与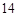 号入选并被分配到同一组的选法种数为
号入选并被分配到同一组的选法种数为
A.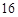 |
B. |
C.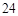 |
D.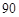 |