(本小题满分13分)
给定椭圆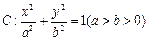 ,称圆心在坐标原点
,称圆心在坐标原点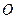 ,半径为
,半径为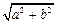 的圆是椭圆
的圆是椭圆 的“伴随圆”. 若椭圆C的一个焦点为
的“伴随圆”. 若椭圆C的一个焦点为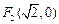 ,其短轴上的一个端点到
,其短轴上的一个端点到 距离为
距离为 .
.
(Ⅰ)求椭圆 及其“伴随圆”的方程;
及其“伴随圆”的方程;
(Ⅱ)若过点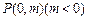 的直线
的直线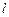 与椭圆C只有一个公共点,且
与椭圆C只有一个公共点,且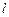 截椭圆C的“伴随圆”所得的弦长为
截椭圆C的“伴随圆”所得的弦长为 ,求
,求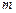 的值;
的值;
(Ⅲ)过椭圆C“伴椭圆”上一动点Q作直线 ,使得
,使得 与椭圆C都只有一个公共点,试判断直线
与椭圆C都只有一个公共点,试判断直线 的斜率之积是否为定值,并说明理由.
的斜率之积是否为定值,并说明理由.
椭圆
经过点
,对称轴为坐标轴,焦点
在
轴上,离心率
。
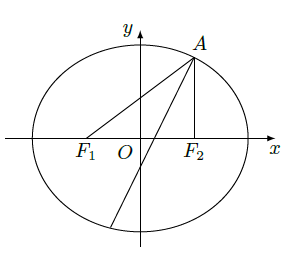
(Ⅰ)求椭圆
的方程;
(Ⅱ)求
的角平分线所在直线
的方程.
的面积是30,内角
所对边长分别为
,
.
(Ⅰ)求
;
(Ⅱ)若
,求
的值.
已知
为半圆
(
为参数,
)上的点,点
的坐标为(1,0),
为坐标原点,点
在射线
上,线段
与
的弧
的长度均为
.
(Ⅰ)以
为极点,
轴的正半轴为极轴建立极坐标系,求点
的坐标;
(Ⅱ)求直线
的参数方程
设
,
分别为椭圆
的左右焦点,过
的直线
与椭圆
相交于
,
两点,直线
的倾斜角为
,
到直线
的距离为
.
(Ⅰ)求椭圆
的焦距;
(Ⅱ)如果
,求椭圆
的方程。
为了比较注射
两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200只家兔随即地分成两组。每组100只,其中一组注射药物
,另一组注射药物
.下表1和表2分别是注射药物A和药物B后的实验结果。(疱疹面积单位:
)
表1:注射药物
后皮肤疱疹面积的频数分布表

表2:注射药物 后皮肤疱疹面积的频数分布表

(Ⅰ)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;

(Ⅱ)完成下面
列联表,并回答能否有99.9%的把握认为"注射药物
后的疱疹面积与注射药物
后的疱疹面积有差异".
表3:

