如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的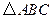 是格点三角形.在建立平面直角坐标系后,点
是格点三角形.在建立平面直角坐标系后,点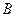 的坐标为(
的坐标为(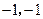 ).
).
(1)把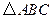 向左平移8格后得到
向左平移8格后得到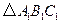 ,画出
,画出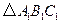 的图形并写出点
的图形并写出点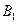 的坐标
的坐标 ;
;
(2)把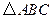 绕点
绕点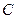 按顺时针方向旋转
按顺时针方向旋转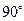 后得到
后得到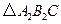 ,画出
,画出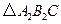 的图形并写出点
的图形并写出点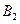 的坐标;
的坐标;
(3)把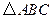 以点
以点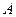 为位似中心放大,使放大前后对应边长的比为
为位似中心放大,使放大前后对应边长的比为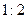 ,画出
,画出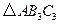 的图形.
的图形.
如图,在直角坐标系 中,直线
中,直线 与
与 轴,
轴, 轴分别交于
轴分别交于 两点,以
两点,以 为边在第二象限内作矩形
为边在第二象限内作矩形 ,使
,使 .
.
(1)求点 ,点
,点 的坐标;
的坐标;
(2)过点 作
作 轴,垂足为
轴,垂足为 ,求证:
,求证: ;
;
(3)求点 的坐标.
的坐标.
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).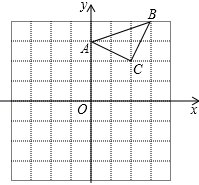
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.
某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出 500千克.经市场调查发现,每千克涨价1元,日销售量将减少20千克.现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
已知:如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m.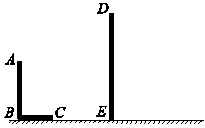
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测出DE在阳光下的投影长为6m,请你计算DE的长.
(1)解方程(1)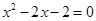 ;
;
(2)已知a≠0,b≠0,且x=1是方程ax2+bx-10=0的一个解,求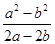 的值.
的值.