如图所示,质量为m,内壁宽度为2L的A盒放在光滑的水平面上(A盒侧壁内侧为弹性材料制成),在盒内底面中点放有质量也为m的小物块B,B与A的底面间的动摩擦因数为 ,某时刻,对B施加一个向右的水平恒力F=
,某时刻,对B施加一个向右的水平恒力F= ,使系统由静止开始运动,当A盒右边缘与墙相撞时,撤去力F,此时B恰好与A右壁相碰。已知A和墙碰撞后速度变为零但不粘连,A和B碰撞过程无机械能损失,假设碰撞时间均极短,求整个过程中:
,使系统由静止开始运动,当A盒右边缘与墙相撞时,撤去力F,此时B恰好与A右壁相碰。已知A和墙碰撞后速度变为零但不粘连,A和B碰撞过程无机械能损失,假设碰撞时间均极短,求整个过程中:
(1)力F做了多少功;
(2)最终物块B的位置离A盒右端的距离。
(1)氢原子的核外电子由离原子核较远的轨道跃迁到离原子核较近的轨道上时,下列说法正确的是()
| A.氢原子的能量增加 | B.氢原子的能量减少 |
| C.氢原子要吸收一定频率的光子 | D.氢原子要放出一定频率的光子 |
(2)将一个质量为3Kg的木板置于光滑水平面上,另一质量为1Kg的物块放在木板上,已知物块和木板之间有摩擦,而木板足够长,若两者都以大小为4m/s的初速度向相反方向运动(如图15所示)则当木板的速度为2.4m/s时,物块的速度为多少?是在加速还是正在减速?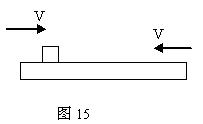
(1)匀速圆周运动属于()
| A.匀速运动 | B.匀加速运动 |
| C.加速度不变的曲线运动 | D.变加速曲线运动 |
(2)如图14所示,滑块在恒定外力作用下从水平轨道上的A点由静止出发,到B点时撤去外力,又沿竖直面内的半月形轨道运动,且恰好通过轨道最高点C,滑块脱离半圆形轨道后又刚好落到原出发点A,试求滑块在AB段运动过程中的加速度。重力加速度为g.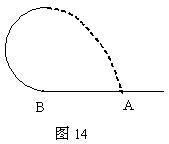
一质量为2Kg木块放在水平面上,木块与水平面的动摩擦因数u=0.5,现在斜向上的拉力F作用下从静止开始做匀加速直线运动,10秒后撤去拉力F,木块便减速到最后静止。已知F=10N,与水平面夹角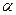 =37°,重力加速度g=10m/s2.求木块总位移和总时间为多少?
=37°,重力加速度g=10m/s2.求木块总位移和总时间为多少?
如图所示,两木块A.B的质量分别为m1和m2,两轻弹簧1、2的劲度系数分别为k1和k2,A压在弹簧1上(但不栓接),整个系统处于平衡状态。现缓慢上提A木块,直到它刚离开1,则在这过程中A木块移动的距离为多少?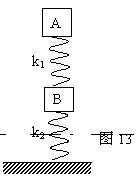
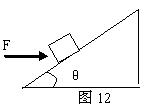
倾角为θ的斜面上有质量为m的木块,它们之间的动摩擦因数为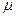 。现用水平力F推动木块,如图12所示,使木块恰好沿斜面向上做匀速运动。若斜面始终保持静止,求水平推力F的大小。
。现用水平力F推动木块,如图12所示,使木块恰好沿斜面向上做匀速运动。若斜面始终保持静止,求水平推力F的大小。