如图所示,在距水平地面h= 0.8m的虚线上方,有方向垂点纸面、水平向内的匀强磁场,正方形线框abcd的边长l=0.2m,质量m= 0.1kg,电阻R=0.08Ω。一条不可伸长的轻绳绕过轻滑轮,一端连线框,另一端连一质量M=0.2kg的物体A。开始时线框的cd边倒好书地面接触,各段绳都处于伸直状态。将A从如图位置由静止释放,一段时间后线框ab边刚进入磁场时恰好做匀速运动,当线框的cd边进入磁场时物体A恰好落地,同时将轻绳剪断,线框在磁场中继续上升一段时间后开始下落,最后落至地面。整个过程线框没有转动,线框平面始终处于纸面内,取g=10m/s2.求:
(1)匀强磁场的磁感应强度B的大小;
(2)线框从开始运动到最高点经历的时间;
(3)线框落地时的速度大小。
扣在水平桌面上的热杯盖有时会发生被顶起的现象;如图,截面积为
的热杯盖扣在水平桌面上,开始时内部封闭气体的温度为
,压强为大气压强
。当封闭气体温度上升至
时,杯盖恰好被整体顶起,放出少许气体后又落回桌面,其内部压强立即减为
,温度仍为
。再经过一段时间,内部气体温度恢复到
。整个过程中封闭气体均可视为理想气体。求: 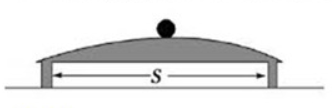
(ⅰ)当温度上升到 且尚未放气时,封闭气体的压强;
(ⅱ)当温度恢复到 时,竖直向上提起杯盖所需的最小力。
如图所示,直径分别为
和
的同心圆处于同一竖直面内,
为圆心,
为大圆的水平直径。两圆之间的环形区域(Ⅰ区)和小圆内部(Ⅱ区)均存在垂直圆面向里的匀强磁场。间距为d的两平行金属极板间有一匀强电场,上极板开有一小孔。一质量为
,电量为
的粒子由小孔下方
处静止释放,加速后粒子以竖直向上的速度
射出电场,由点紧靠大圆内侧射入磁场。不计粒子的重力。 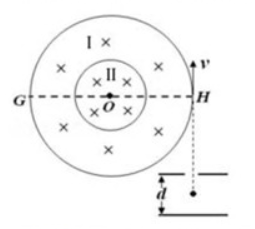
(1)求极板间电场强度的大小;
(2)若粒子运动轨迹与小圆相切,求区磁感应强度的大小;
(3)若Ⅰ区,Ⅱ区磁感应强度的大小分别为 , ,粒子运动一段时间后再次经过 点,求这段时间粒子运动的路程。
如图甲所示,物块与质量为
的小球通过不可伸长的轻质细绳跨过两等高定滑轮连接。物块置于左侧滑轮正下方的表面水平的压力传感装置上,小球与右侧滑轮的距离为
。开始时物块和小球均静止,将此时传感装置的示数记为初始值。现给小球施加一始终垂直于
段细绳的力,将小球缓慢拉起至细绳与竖直方向成
角,如图乙所示,此时传感装置的示数为初始值的1.25倍;再将小球由静止释放,当运动至最低位置时,传感装置的示数为初始值的0.6倍.不计滑轮的大小和摩擦,重力加速度的大小为
。求: 
(1)物块的质量;
(2)从释放到运动至最低位置的过程中,小球克服阻力所做的功。
如图所示,一条带有圆轨道的长轨道水平固定,圆轨道竖直,底端分别与两侧的直轨道相切,半径 ,物块 以 的速度滑入圆轨道,滑过最高点 ,再沿圆轨道滑出后,与直轨道上 处静止的物块 碰撞,碰后粘在一起运动, 点左侧轨道光滑,右侧轨道呈粗糙段、光滑段交替排列,每段长度都为 ,物块与各粗糙段间的动摩擦因数都为 , 、 的质量均为 (重力加速度 取 ; 、 视为质点,碰撞时间极短)。

⑴求 滑过Q点时的速度大小 和受到的弹力大小 ;
⑵若碰后 最终停止在第 个粗糙段上,求 的数值;
⑶求碰后
滑至第
个
光滑段上的速度
与
的关系式。
如图(
)所示,平行长直金属导轨水平放置,间距
,导轨右端接有阻值
的电阻,导体棒垂直放置在导轨上,且接触良好,导体棒及导轨的电阻均不计,导轨间正方形区域
内有方向竖直向下的匀强磁场,
连线与导轨垂直,长度也为
,从0时刻开始,磁感应强度
的大小随时间
变化,规律如图(
)所示;同一时刻,棒从导轨左端开始向右匀速运动,
后刚好进入磁场,若使棒在导轨上始终以速度
做直线运动,求:
⑴棒进入磁场前,回路中的电动势
;
⑵棒在运动过程中受到的最大安培力
,以及棒通过三角形
区域时电流
与时间
的关系式。