（（本小题满分12分）
如图，已知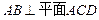
，
，
，
,
．
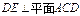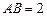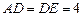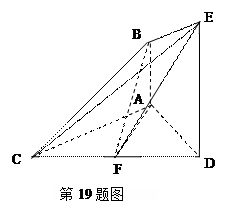
（Ⅰ）求证：
;
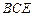(Ⅱ) 若
，求二面角 
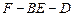的余弦值．
（1）已知命题
和命题
,若
是
的必要不充分条件,求实数
的取值范围.
（2）已知命题
方程
的一根在
内,另一根在
内.
命题
函数
的定义域为全体实数.
若
为真命题,求实数
的取值范围.
某年某省有
万多文科考生参加高考,除去成绩为
分（含分）以上的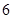
人与成绩为
分（不含分）以下的
人,还有约
万文科考生的成绩集中在
内,其成绩的频率分布如下表所示：
| 分数段 |
 |
 |
 |
 |
| 频率 |
0.108 |
0.133 |
0.161 |
0.183 |
| 分数段 |
 |
 |
 |
 |
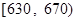| 频率 |
0.193 |
0.154 |
0.061 |
0.007 |
（1）请估计该次高考成绩在内文科考生的平均分（精确到
）；
（2）考生A填报志愿后,得知另外有4名同分数考生也填报了该志愿.若该志愿计划录取2人,并在同分数考生中随机录取,求考生A被该志愿录取的概率.
（参考数据：610×0.061+570×0.154+530×0.193+490×0.183+450×0.161+410×0.133=443.93）
在
中,角
的对边分别为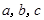
,且满足
（1）求证：
；
（2）若的面积
,
,
的值.
已知函数
.
（1）求函数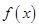
在区间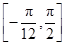
上的最大值和最小值；
（2）若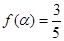
,其中
求
的值.
已知函数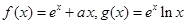
（
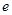是自然对数的底数）.
（1）若曲线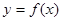
在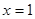
处的切线也是抛物线
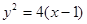的切线，求
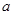的值；
（2）当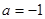
时，是否存在
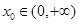，使曲线
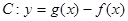在点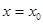
处的切线斜率与
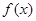在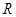
上的最小值相等？若存在，求符合条件的
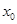的个数；若不存在，请说明理由.