两个靠得很近的恒星称为双星,这两颗星必定以一定角速度绕二者连线上的某一点转动才不至于由于万有引力的作用而吸引在一起,已知两颗星的质量分别为M、m ,相距为L,试求:(1)两颗星转动中心的位置;(2)这两颗星转动的周期。
如图所示,直角三棱镜的折射率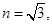 ∠A=30°,一束与OB面成300角的光射向OB面,从AB面上的C点射出.若不考虑光在OB面上的反射,求能从C点射向空气的光的方向.
∠A=30°,一束与OB面成300角的光射向OB面,从AB面上的C点射出.若不考虑光在OB面上的反射,求能从C点射向空气的光的方向.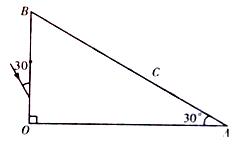
如图所示,体积为V、内壁光滑的圆柱形导热气缸顶部有一质量和厚度均可忽略的活塞;气缸内密封有温度为2.4T0、压强为1.2P0的理想气体.P0和T0分别为大气的压强和温度.已知:气体内能U与温度T的关系为U=aT,a为正的常量;容器内气体的所有变化过程都是缓慢的,求:
(1)缸内气体与大气达到平衡时的体积V1;
(2)在活塞下降过程中,气缸内气体放出的热量Q.
如图所示为一利用传输带输送货物的装置.物块(视为质点)自平台经斜面滑到一以恒定速度v运动的水平长传输带上,再由传输带输送到远处目的地.已知斜面高h=2.0m,水平边长L=4.0m,传输带宽d=2.0m,传输带的运动速度v=3.0m/s,物块与斜面间的摩擦系数μ1=0.30,物块自斜面顶端下滑的初速度为零,沿斜面下滑的速度方向与传输带运动方向垂直.设物块通过斜面与传输带交界处时无动能损失.重力加速度g=10m/s2.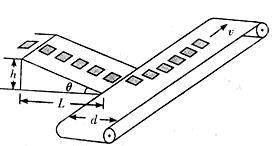
(1)为使物块滑到传输带上后不会从传输带边缘脱离,物块与传输带之间的摩擦系数μ2至少为多少?
(2)当货物的平均流量(单位时间里输送的货物质量)稳定在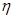 =40kg/s时,求单位时间里物块对传输带所做的功W1以及传输带对物块所做功W2。
=40kg/s时,求单位时间里物块对传输带所做的功W1以及传输带对物块所做功W2。
如图所示,地面和半圆轨道面均光滑。质量M =" 1kg" 、长L = 4m的小车放在地面上,其右端与墙壁的距离为S=3m,小车上表面与半圆轨道最低点P的切线相平。现有一质量m = 2kg的滑块(视为质点)以v0 = 6m/s的初速度滑上小车左端,带动小车向右运动。小车与墙壁碰撞时即被粘在墙壁上,已知滑块与小车表面的滑动摩擦因数μ =" 0.2" ,g取10m/s2。
(1)求小车与墙壁碰撞时的速度;
(2)要使滑块在半圆轨道上运动时不脱离,求半圆轨道的半径R的取值.
试将一天的时间记为T,地球半径记为R,地球表面重力加速度为g.(结果可保留根式)
(1)试求地球同步卫星P的轨道半径RP;
(2)若已知一卫星Q位于赤道上空且卫星Q运动方向与地球自转方向相反,赤道上一城市A的人平均每三天观测到卫星Q四次掠过他的上空,试求Q的轨道半径RQ