对于定义在R上的函数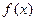 ,有下述命题:
,有下述命题:
①若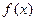 是奇函数,则
是奇函数,则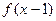 的图象关于点A(1,0)对称
的图象关于点A(1,0)对称
②若函数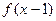 的图象关于直线
的图象关于直线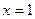
 对称,则
对称,则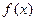 为偶函数
为偶函数
③若对 ,有
,有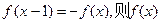 的周期为2
的周期为2
④函数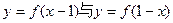 的图象关于直线
的图象关于直线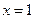 对称.
对称.
其中正确命题的个数是( )
A . 1 B . 2 C . 3 D . 4
用数学归纳法证明不等式 成立,起始值至少应取为()
成立,起始值至少应取为()
| A.7 | B.8 | C.9 | D.10 |
设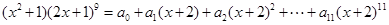 ,
,
则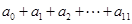 的值为( )
的值为( )
A.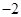 |
B. |
C. |
D.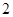 |
平面上有 条直线,其中任意两条不平行,任意三条不共点。
条直线,其中任意两条不平行,任意三条不共点。 表示
表示 时平面被分成的区域数,则
时平面被分成的区域数,则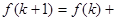 ( )
( )
A. |
B.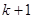 |
C.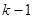 |
D.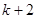 |
“因为指数函数 是增函数(大前提),而
是增函数(大前提),而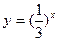 是指数函数(小前提),所以
是指数函数(小前提),所以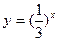 是增函数(结论)”,上面推理的错误是( )
是增函数(结论)”,上面推理的错误是( )
| A.大前提错导致结论错 | B.小前提错导致结论错 |
| C.推理形式错导致结论错 | D.大前提和小前提错都导致结论错 |
已知定义在R上的函数 满足下列三个条件
满足下列三个条件
①对于任意的 都有
都有 ;
;
②对于任意的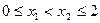 都有
都有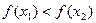 ;
;
③函数 的图像关于
的图像关于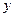 轴对称。则下列结论正确的是
轴对称。则下列结论正确的是
A.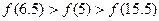 |
B.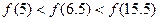 |
C.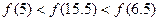 |
D.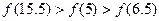 |