(本小题满分10分)选修4-5:不等式选讲
设 (
( ).
).
(Ⅰ)当 时,求函数
时,求函数 的定义域;
的定义域;
(Ⅱ)若当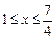 ,
, 恒成立,求实数
恒成立,求实数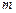 的取值范围.
的取值范围.
如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).
(1)求证:平面EFG∥平面PAB;
(2)若点Q是线段PB的中点,求证:PC⊥平面ADQ;
(3)求三棱锥C-EFG的体积.
如图, 是半径为
是半径为 的半圆,
的半圆,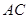 为直径,点
为直径,点 为
为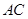 的中点,点
的中点,点 和点
和点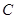 为线段
为线段 的三等分点,平面
的三等分点,平面 外一点
外一点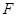 满足
满足 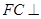 平面
平面 ,
, .
.
(1)证明: ;
;
(2)求点 到平面
到平面 的距离.
的距离.
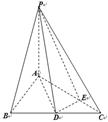
如图,三角形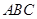 是边长为4的正三角形,
是边长为4的正三角形,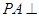 底面
底面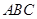 ,
, ,点
,点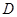 是
是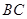 的中点,点
的中点,点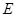 在
在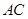 上,且
上,且 .
.
(1)证明:平面 平面
平面 ;
;
(2)求直线 和平面
和平面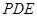 所成角的正弦值.
所成角的正弦值.
如图,在边长为1的正方体ABCD-A1B1C1D1中,求证:
(1)A1C^平面BDC1;
(2)求三棱锥A1—BDC1的体积。
长方体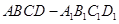 中,
中, ,
, ,点
,点 为
为 中点.
中点.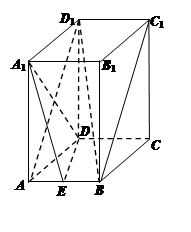
(Ⅰ)求证:
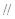 平面
平面 ;
;
(Ⅱ)求证: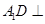 平面
平面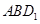 ;
;