如图,xOy平面内有一以原点O为圆心的圆,动点P在圆周上沿顺时针方向做速度大小始终为v的圆周运动,另一动点Q沿x轴正方向做匀速直线运动。A、B为圆与x轴的交点,某时刻P、Q在A点相遇,经过一段时间后又在B点相遇,则Q的速度大小为 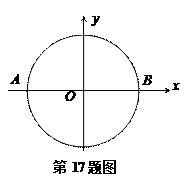
(14分)(2013成都检测)如右图所示,一带电微粒质量为m=2.0×10-11kg、电荷量q=+1.0×10-5C,从静止开始经电压为U1=100 V的电场加速后,从两平行金属板的中间水平进入偏转电场中,微粒从金属板边缘射出电场时的偏转角θ=30°,并接着进入一个方向垂直纸面向里、宽度为D=34.6 cm的匀强磁场区域.微粒重力忽略不计.求:
(1)带电微粒进入偏转电场时的速率v1;
(2)偏转电场中两金属板间的电压U2;
(3)为使带电微粒不会由磁场右边射出,该匀强磁场的磁感应强B至少多大?
(10分)如图所示,绝缘直棒上的小球,其质量为m,带电荷量为+q,小球可在棒上滑动.将此棒竖直放在相互正交的匀强电场和匀强磁场中,电场强度为E,磁感应强度为B,小球与直棒间的动摩擦因数为μ,求小球由静止沿棒下滑的最大加速度和最大速度.(小球带电荷量不变)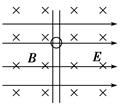
(8分)如图所示,质量为m,带电量为+q的粒子,从两平行电极板正中央垂直电场线和磁感线以速度v飞入.已知两板间距为d,磁感应强度为B,这时粒子恰能沿直线穿过电场和磁场区域(重力不计).今将磁感应强度增大到某值,则粒子将落到极板上.当粒子落到极板上时的动能为多大?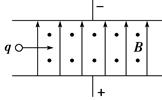
(8分)如图所示,两根平行金属导轨M、N,电阻不计,相距0.2 m,上边沿导轨垂直方向放一个质量为m=5×10-2kg的金属棒ab,ab的电阻为0.5 Ω.两金属导轨一端通过电阻R和电源相连.电阻R=2 Ω,电源电动势E=6 V,电源内阻r=0.5 Ω,如果在装置所在的区域加一个匀强磁场,使ab对导轨的压力恰好是零,并使ab处于静止.(导轨光滑)求所加磁场磁感强度的大小和方向.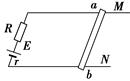
如图所示,光滑水平面上固定一倾斜角为30o的光滑斜面,紧靠斜面底端有一质量为4kg的木板,木板与斜面底端之间通过微小弧形轨道相接,以保证滑块从斜面滑到木板的速度大小不变。质量为2kg的滑块从斜面上高h=1.8m处由静止滑下,并以到达倾斜底端的速度滑上木板左端,最终滑块没有从木板上滑下。已知滑块与木板间的动摩擦因数μ=0.2,取g=10m/s2求:(1)滑块从滑上木板到与木板速度相同经历的时间(2)木板的最短长度;