给定下列四个命题：
①若一个平面内的两条直线与另一个平面都平行，则这两个平面平行；
②若两个平面都垂直于同一条直线，则这两个平面平行；
③若两个平面互相垂直，则在其中一个平面内的直线垂直另外一个平面；
④若两个平面互相平行，则在其中一个平面内的直线平行另外一个平面．
其中为真命题的是
| A．①和② | B．②和③ | C．③和④ | D．②和④ |
设a∈R，函数f(x)＝x3＋ax2＋(a－3)x的导函数是 f ’(x)，若f ’( x )是偶函数，则曲线
y＝f (x) 在原点处的切线方程为（）
| A．y＝－3x | B．y＝－2x | C．y＝3x | D．y＝2x |
等差数列
n
的前几项和为Sn，且S3＝6，a3＝4，则公差d等于（）
| A．1 | B． |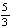
C．2 | D．3 |
设变量x，y满足约束条件
则目标函数z＝2x+3y的最小值为 （）
| A．6 | B．7 | C．8 | D．23 |
为了得到函数y＝lg
的图像，只需把函数y＝lgx的图像上所有的点 （）
| A．向左平移3个单位长度，再向上平移1个单位长度 |
| B．向右平移3个单位长度，再向上平移1个单位长度 |
| C．向左平移3个单位长度，再向下平移1个单位长度 |
| D．向右平移3个单位长度，再向下平移1个单位长度 |
已知tanα＝4，cotβ＝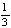
，则tan（α＋β）等于（）
A． |
B．－ |
C． |
D．－ |