相距L＝1.5m的足够长金属导轨竖直放置，质量为m1＝1.0kg的金属棒ab和质量为m2＝0.27kg的金属棒cd均通过棒两端的套环水平地套在金属导轨上，如图（a）所示，虚线上方磁场方向垂直纸面向里，虚线下方磁场方向竖直向下，两处磁场磁感应强度大小相同。ab棒光滑，cd棒与导轨间动摩擦因数为μ＝0.75，两棒总电阻为R=1.8Ω，导轨电阻不计。ab棒在方向竖直向上，大小按图（b）所示规律变化的外力F作用下，从静止开始，沿导轨匀加速运动，同时cd棒也由静止释放。取重力加速度g=10m/s2。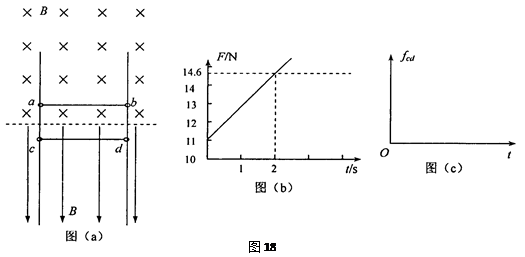
（1）求出磁感应强度B的大小和ab棒加速度大小；
（2）已知在2 s内外力F做功40 J，求这一过程中两金属棒产生的总焦耳热；
（3）判断cd棒将做怎样的运动，求出cd棒达到最大速度所需的时间t0，并在图（c）中定性画出cd棒所受摩擦力fcd随时间变化的图象。
2011年7月23日，发生在温州的动车追尾事故造成重大的人员伤亡和经济损失。有报道称，在紧急关头，D301次列车司机放弃逃生，紧急制动使列车尽量降速，使得列车相撞的冲击力大大降低，他用生命挽救了许多人和许多家庭。据资料记载进行估算，当时火车以216km/h行进，制动后以180km/h与静止的前车相撞，该动车制动时最大能产生1m/s2的加速度。司机从发现险情，需0.7s的反应时间，采取措施紧急制动。根据以上信息，估算列车司机是在距相撞地点多少米处，发现前方静止的列车的？
汽车在平直的公路上运动，它先以速度v行驶了2/3的位移，接着以20m/s的速度驶完余下1/3位移，若全程的平均速度是30m/s，则v的大小为？
10分）一质点原来以6m/s的速度做匀速直线运动，从t=0时刻开始做匀变速直线运动，在前4s内该质点前进了8m。在t=5s时，该质点开始做匀速运动，在最后2s的时间内质点匀减速到静止。整个过程中，该质点的位移大小为3m。求：
（1）5s后质点匀速运动时的速度是多大？方向如何？
（2）在匀减速阶段该质点的加速度是多大？方向如何？
（3）第7s时该质点的速度是多大？方向如何？
（4）作出整个过程中该质点运动的
图象。
一辆汽车在十字路口等候绿灯，当绿灯亮时，汽车以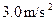
的加速度开始行驶，恰在此时一辆自行车以
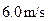的速度匀速驶来，从后面赶过汽车．求：
（1）什么时候汽车追上自行车？
（2）汽车追上自行车时，汽车的速度是多大？
10分）以
的速度行驶的汽车，制动刹车后做匀减速运动，在
内前进
．求：
（1）汽车的加速度；
（2）从汽车开始刹车时计时，5.0
内汽车前进的距离．