如图21所示,第四象限内有互相正交的匀强电场E与匀强磁场B1,E的大小为1.5×103V/m,Bl大小为0.5T;第一象限的某个矩形区域内,有方向垂直纸面的匀强磁场B2,磁场的下边界与x轴重合。一质量m=1×10-14kg、电荷量q=2×l0-10C的带正电微粒以某一速度v沿与y轴正方 向60°角
向60°角 从M点沿直线运动,经P点即进入处于第一象限内的磁场B2区域。一段时间后,小球经过y轴上的N点并与y轴正方向成60°角的方向飞出。M点的坐标为(0,-10),N点的坐标为(0,30),不计粒子重力,g取10m/s2。则求:
从M点沿直线运动,经P点即进入处于第一象限内的磁场B2区域。一段时间后,小球经过y轴上的N点并与y轴正方向成60°角的方向飞出。M点的坐标为(0,-10),N点的坐标为(0,30),不计粒子重力,g取10m/s2。则求:
(1)微粒运动速度v的大小;
(2)匀强磁场B2的大小;
(3)B2磁场区域的最小面积。
某市规定卡车在市区一特殊路段的速度不得超过36k m/h。有一辆卡车在危急情况下紧急刹车,车轮抱死滑动一段距离后停止。交警测得刹车过程中车轮在路面上擦过的笔直的痕迹长是9m。从厂家的技术手册中查得该车轮胎和地面的动摩擦因数是0.8 ,
m/h。有一辆卡车在危急情况下紧急刹车,车轮抱死滑动一段距离后停止。交警测得刹车过程中车轮在路面上擦过的笔直的痕迹长是9m。从厂家的技术手册中查得该车轮胎和地面的动摩擦因数是0.8 ,
①假若你就是这位交警,请你判断卡车是否超速行驶?(假定刹车后卡车做匀减速直线运动)
②减小刹车距离是避免交通事故的最有效的途径。刹车距离除与汽车的初速度、制动力有关外,还须考虑驾驶员的反应时间:即从发现情况到肌肉动作操纵制动器的时间。假设汽车刹车制动力是定值f,驾驶员的反应时间为t0,汽车的质量为m,行驶的速度为v0,请你给出刹车距离s的表达式。
皮带运输机是靠货物和传送带之间的摩擦力把货物送往别处的.如图12所示,已知传送带与水平面的倾角为θ=37°,以4m/s的速率向上运行,在传送带的底端A处无初速地放上一质量为0.5kg的物体,它与传送带间的动摩擦因数为0.8.若传送带底端A到顶端B的长度为25m,则物体从A到B的时间为多少?(取g=10 m/s2,sin37°=0.6)
质量为3 kg的物体,在0 ~ 4 s内受水平力F的作用,在4 ~ 10 s 内因受摩擦力作用而停止,其v-t图象如图所示。求:
内因受摩擦力作用而停止,其v-t图象如图所示。求:
(1)物体所受的摩擦力。
(2)在0 ~ 4 s内物体所受的拉力。
(3)在0 ~ 10 s内物体的位移。
 如图所示,质量为m=4kg的物体与水平地面间的动摩擦因数μ=0.2,现用F=25N与水平方向成θ=370的力拉物体,使物体由静止开始做匀加速运动:
如图所示,质量为m=4kg的物体与水平地面间的动摩擦因数μ=0.2,现用F=25N与水平方向成θ=370的力拉物体,使物体由静止开始做匀加速运动:
(1)求物体的加速度的大小?
(2)若F作用t=4s后即撤除,此后物体还能运动多久?
(sin37°=0.6,cos37°=0.8,g="10" m/s2)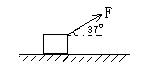
光滑水平地面上停放着甲、乙两辆相同的平板车,一根轻绳跨过乙车的定滑轮(不计定滑轮的质量和摩擦),绳的一端与甲车相连,另一端被甲车上的人拉在手中,已知每辆车和人的质量均为30kg,两车间的距离足够远。现在人用力拉绳,两车开始相向运动,人与甲车保持相对静止,当乙车的速度为0.5m/s时,停止拉绳。求:
(1)人在拉绳过程做了多少功?
(2)若人停止拉绳后,至少以多大速度立即从甲车跳到乙车才能使两车不发生碰撞?