（1）如图所示，MN是位于竖直平面内的光屏，放在水平面上的半圆柱形玻璃砖的平面部分ab与屏平行．由光源S发出的一束白光从半圆沿半径射入玻璃砖，通过圆心O再射到屏上．在水平面内以O点为圆心沿逆时针方向缓缓转动玻璃砖，在光屏上出现了彩色光带．当玻璃砖转动角度大于某一值，屏上彩色光带中的某种颜色的色光首先消失．有关彩色的排列顺序和最先消失的色光是（ ）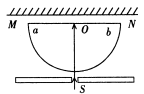
A．左红右紫，红光 B．左红右紫，紫光 C．左紫右红，红光 D．左紫右红，紫光
（2）A、B两点相距6m，A处有一个做简谐振动的波源，当空间充有某种介质时，A点的振动经过0.5s传播到B点，此后A、B两点的振动方向始终相反；若空间充有另一种介质时，A点的振动经过0.6s传播到B点，此后A、B两点的振动始终相同，求这波源振动的最小频率。
质量为2千克的物体，静止在水平地面上，物体与地面之间的动摩擦因数为0.5，给物体一水平拉力，物体与地面的最大静摩擦力为12N，求：
⑴当拉力大小为11N时，地面对物体的摩擦力是多大？
⑵当拉力大小为15N时，地面对物体的摩擦力是多大？
⑶此后若将拉力减小为5N(物体仍在滑动)，地面对物体的摩擦力是多大？（g取10N/kg）
矿井里的升降机，从静止开始匀加速上升，经过3s速度达到3m/s，然后以这个速度匀速上升了25m,最后匀减速上升，经过2s到达井口，正好停下来，求矿井的深度？
（12分)如图所示，AB是一段位于竖直平面内的光滑轨道，高度为h，末端B处的切线方向水平．一个质量为
的小物块P从轨道顶端A处由静止释放，滑到B端后飞出，落到地面上的C点，轨迹如图中虚线BC所示．己知它落地时相对于B点的水平位移OC= 
．现在轨道下方紧贴B点安装一水平传送带，传送带的右端与B的距离为，／2．当传送带静止时，让P再次从A点由静止释放，它离开轨道并在传送带上滑行后从右端水平飞出，仍然落在地面的C点．当驱动轮转动从而带动传送带以速度
匀速向右运动时(其它条件不变)。P的落地点为D．(不计空气阻力)
(1)求P滑至B点时的速度大小：
(2)求P与传送带之间的动摩擦因数：
(3)用S-V图象表示出O、D间的距离S随速度V变化的关系。（不要求写出具体运算过程）
如图所示,左图是杭州儿童乐园中的过山车的实物图片,右图是过山车的原理图.在原理图中,半径分别为R1="2.0" m和R2="8.0" m的两个光滑圆形轨道固定在倾角为
=37°斜轨道面上的Q、Z两点,且两圆形轨道的最高点A、B均与P点平齐,圆形轨道与斜轨道之间圆滑连接.现使质量
的小车(视作质点)从P点以一定的初速度沿斜轨道向下运动.已知斜轨道面与小车间的动摩擦因数为
=
,g="10" m/s2,sin 37°="0.6,cos" 37°=0.8.问:
(1)若小车能通过A、B两点,则小车在P点的初速度满足什么条件？
(2)若小车恰好能通过第二个圆形轨道的最高点B,则小车通过第一个圆形轨道最低点
时，对轨道的压力大小是多少?
质量为40kg的雪撬在倾角θ=37°的斜面上向下滑动，如图甲所示，所受的空气阻力与速度成正比。今测得雪撬运动的v-t图象如图乙所示，且AB是曲线的切线，B点坐标为（4，15），CD是曲线的渐近线。试求空气的阻力系数k和雪撬与斜坡间的动摩擦因数μ（g="10" m/s2）