如图所示,传送带以v为l0m/s速度向左匀速运行,BC段长L为2m,半径R为1.8m的光滑圆弧槽在B点与水平传送带相切.质量m为0.2kg的小滑块与传送带间的动摩擦因数为0.5,g取l0m/s2,不计小滑块通过连接处的能量损失.求:
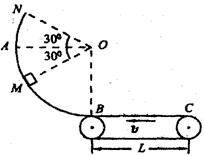
(1) 小滑块从M处无初速度滑下,到达底端B时的速度;
(2) 小滑块从M处无初速度滑下后,在传送带上向右运动的最大距离及此过程产生的
热量;
(3) 将小滑块无初速度放在传送带C端,要使小滑块能通过N点,传送带BC段至少为多长?
A、B两车在同一直线上向右匀速运动,B车在A车前,A车的速度大小为V1=8m/s, B车的速度大小为V2=20m/s,如图所示。当A、B两车相距x0=28m时,B车因前方突发情况紧急刹车(已知刹车过程的运动可视为匀减速直线运动),加速度大小为a=2m/s2,从此时开始计时,求:
(1)A车追上B车之前,两者相距的最大距离;
(2)A车追上B车所用的时间;
(3)从安全行驶的角度考虑,为避免两车相撞,在题设条件下,A车在B车刹车的同时也应刹车的最小加速度.
如图所示,直杆长L1=0.5m,圆筒高为L2=3.7m。直杆位于 圆筒正上方H=0.8m处。直杆从静止开始做自由落体运动,并能竖直穿越圆筒。试求:直杆穿越圆筒所用的时间t(取g=10m/s2)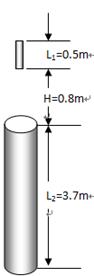
一列火车进站前先关闭气阀(动力系统),让车沿直线滑行,滑行了225m时,速度恰为关闭气阀时速度的一半,此后,又继续沿直线滑行了30s,停止在车站,设火车在滑行过程中加速度始终保持不变,试求:
(1)火车从关闭气阀到停止滑行时,滑行的总位移大小;
(2)火车滑行的加速度大小.
(12分,特殊班做,普通班不做)某汽车训练场地有如图设计,在平直的道路上,依次有编号为A、B、C、D、E的五根标志杆,相邻杆之间的距离ΔL=12.0 m。一次训练中,学员驾驶汽车以57.6km/h的速度匀速向标志杆驶来,教练与学员坐在同排观察并记录时间。当教练经过O点时向学员发出指令:“立即刹车”,同时用秒表开始计时。忽略反应时间,刹车后汽车做匀减速直线运动,停在D标杆附近。教练记录自己经过C杆时秒表的读数为tC=6.0 s,已知LOA=36m,教练距车头的距离Δs=1.5 m。求: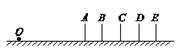
(1)刹车后汽车做匀减速运动的加速度大小a;
(2)汽车停止运动时,车头离标志杆D的距离Δx.
(12分,普通班做,特殊班不做)一物体做匀加速直线运动,初速度v0 = 5m/s,加速度a = 0.5m/s2,求物体在第3s内的位移大小.