劲度系数为20N/cm的弹簧振子,它的振动图象如图所示,在图中A点对应的时刻( )
| A.振子所受的弹力大小为0.5N,方向指向x轴的负方向 |
| B.振子的速度方向指向x轴的正方向 |
C.在0~4s内 振子作了1.75次全振动 振子作了1.75次全振动 |
| D.在0~4s内振子通过的路程为0.35cm,位移为0 |
英国物体学家麦克斯韦认为,磁场变化时会在空间激发感生电场,如图所示,一个半径为r的绝缘细圆环放置,环内存在竖直向上的匀强磁场,环上套一带电荷量为 的小球,已知磁感强度 随时间均匀增加,其变化率为 ,若小球在环上运动一周,则感生电场对小球的作用力所做功大小是()
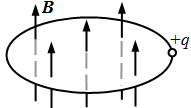
| A. | B. | C. | D. |
如图所示,一倾斜的匀质圆盘垂直于盘面的固定对称轴以恒定的角速度 转动,盘面上离转轴距离2.5 处有一小物体与圆盘始终保持相对静止,物体与盘面间的动摩擦因数为 。设最大静摩擦力等于滑动摩擦力),盘面与水平面间的夹角为30°, 取10 。则 的最大值是()
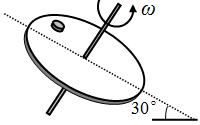
| A. | B. | C. | 1.0 | D. | 0.5 |
"人造小太阳"托卡马克装置使用强磁场约束高温等离子体,使其中的带电粒子被尽可能限制在装置内部,而不与装置器壁碰撞,已知等离子体中带电粒子的平均动能与等离子体的温度 成正比,为约束更高温度的等离子体,则需要更强的磁场,以使带电粒子在磁场中的运动半径不变,由此可判断所需的磁感应强度B正比于()
| A. | B. | C. | D. |
一带电粒子在电场中仅受静电力作用,做初速度为零的直线运动,取该直线为 轴,起始点 为坐标原点,其电势能 与位移 的关系如图所示,下列图象中合理的是()

| A. |
粒子所处位置电势与位移关系 |
B. |
粒子动能与位移关系 |
| C. |
粒子速度与位移关系 |
D. |
粒子加速度与位移关系 |
一简谐横波沿 轴正向传播,图1是 =0时刻的波形图,图2是介质中某质点的振动图象,则该质点的 坐标值合理的是()

| A. | 0.5 | B. | 1.5 | C. | 2.5 | D. | 3.5 |