某同学设想用带电粒子的运动轨迹做出“0”、“8”字样，首先，如图甲所示，在真空空间的竖直平面内建立xoy坐标系，在y1=0.1m和y2= -0.1m处有两个与x轴平行的水平界面PQ和MN把空间分成Ⅰ、Ⅱ、Ⅲ三个区域，在三个区域中分别存在匀强磁场B1、B2、B3，其大小满足B2=2B1=2B3=0.02T，方向
如图甲所示。在Ⅱ区域中的y轴左右两侧还分别存在匀强电场E1、E2（图中未画出），忽略所有电、磁场的边缘效应. ABCD是以坐标原点O为中心对称的正方形，其边长L=0.2m。现在界面PQ上的A处沿y轴正方向发射一比荷q/m=108c/kg的带正电荷的粒子（重力不计），粒子恰能沿图中实线途经B、C、D三点后回到A点并做周期性运动，轨迹构成一个“0”字.己知粒子每次穿越Ⅱ区域时均做直线运动.
（1）求E1、E2场的大小和方向
（2）若去掉Ⅱ和Ⅲ区域中的匀强电场和磁场，其他条件不变，仍在
处以相同的速度发射相同的粒子，请在Ⅱ和Ⅲ区域内重新设计适当的匀强电场或匀强磁场，使粒子运动的轨迹成为上、下对称的“8”字，且粒子运动的周期跟甲图中相同，请通过必要的计算和分析，求出你所设计的“场”的大小、方向和区域，并在乙图中描绘出带电粒子的运动轨迹和你所设计的“场”（上面半圆轨迹己在图中画出）
如图，是《驾驶员守则》中的安全距离图示和部分安全距离表格：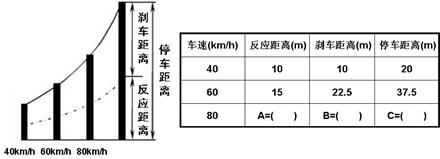
请根据图表计算
（1）如果驾驶员的反应时间一定、路面情况相同，请在表格中填入A、B、C的数据；
（2）如果路面情况相同，一名喝了酒的驾驶员发现前面50m处有一队学生正在横穿马路，此时他的车
速为72km/h，而他的反应时间比正常时慢了0.1s，请问他能在50m内停下来吗？
一光滑圆环固定在竖直平面内，环上套着两个小球A和B（中央有孔），A、 B间由细绳连接着，它们处于如图所示位置时恰好都能保持静止状态。此情况下， B球与环中心O处于同一水平面上，A、B间的细绳呈伸直状态，与水平线成300夹角。已知B球的质量为m，求细绳对B球的拉力和A球的质量。
中国海军网9月25日上午发布消息，9月25日上午，中国首艘航空母舰“辽宁号”正式交接入列。辽宁号参数：主尺寸：舰长304米、水线281米；舰宽70.5米、吃水10.5米；飞行甲板：长300米、宽70米；排水量：57000吨（标准），67500吨（满载）；若采用舰载机为国产歼15机型，设该型号飞机的起飞速度为50m/s。假设该航空母舰静止在某海面上
(1)飞机发动机需要给飞机提供至少多大的加速度？
(2)若飞机的加速度是5 m/s2，要使飞机达到起飞速度需要多大的起飞距离？
带有等量异种电荷的两块水平金属板M、N正对放置，相距为d（d远小于两板的长和宽），一个带正电的油滴A恰好能悬浮在两板正中央，如图所示。A的质量为m，所带电荷量为q，在A正上方距离M板2d处，有另一质量也为m的带电油滴B由静止释放，可穿过M板上的小孔进入两板间，若能与油滴A相碰，会结合成一个油滴，结合后的瞬间该油滴的速度为碰前油滴B速度的一半，方向竖直向下。整个装置放在真空环境中，不计油滴B和A间的库仑力以及金属板的厚度，为使油滴B能与油滴A相碰且结合后不会与金属板N接触，重力加速度取g，求：
（1）金属板M、N间的电压U的大小；
（2）油滴B带何种电荷？请简要说明理由；
（3）油滴B所带电荷量的范围。
如图所示，固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷，电荷量分别为＋Q和－Q，A、B相距为2d．MN是竖直放置的光滑绝缘细杆，另有一个穿过细杆的带电小球p，其质量为m、电荷量为+q（可视为点电荷，不影响电场的分布．），现将小球p从与点电荷A等高的C处由静止开始释放，小球p向下运动到距C点距离为d的O点时速度为v，已知MN与AB之间的距离为d，静电力常量为k，重力加速度为g．求：
（1）C、O间的电势差UCO；
（2）小球p在O点时的加速度；
（3）小球p经过与点电荷B等高的D点时的速度大小．