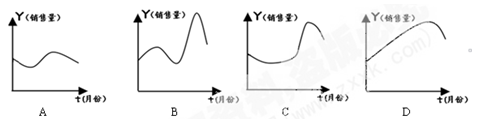
用数学归纳法证明“(n＋1)(n＋2)·…·(n＋n)＝2n·1·3·…·(2n－1)”，从“k到k＋1”左端需增乘的代数式为( )
A．2k＋1 B．2(2k＋1)
C. D.
已知P(x,y)为椭圆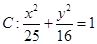
上一点,F为椭圆C的右焦点,若点M满足
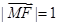且
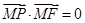,则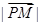
的最小值为( )
A． |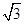
B．3 | C． |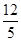
D．1 |
已知直线a,b异面, ,给出以下命题：①一定存在平行于a的平面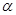
使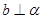
;②一定存在平行于a的平面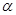使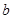
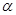∥;③一定存在平行于a的平面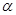使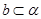
;④一定存在无数个平行于a的平面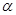与b交于一定点.则其中论断正确的是( )
| A．①④ | B．②③ | C．①②③ | D．②③④ |
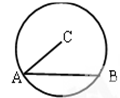
如图,半径为R的圆C中,已知弦AB的长为5,则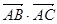
=( )
A． |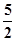
B． |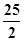
C． |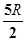
D． |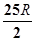
函数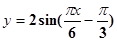
(0≤x≤9)的最大值与最小值的和为( ).
A． |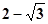
B．0 | C．－1 | D． |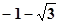
某公司的一品牌电子产品,2013年年初,由于市场疲软,产品销售量逐渐下降,五月份公司加大了宣传力度,销售量出现明显的回升,九月份,公司借大学生开学之际,采取了促销等手段,产品的销售量猛增,十一月份之后,销售量有所回落.下面大致能反映出公司2013年该产品销售量的变化情况的图象是( )