某商场销售一批名牌衬衫,平均每天可以售出20件,每件盈利40元,为了扩大销售量,增加盈利,尽快减少库存,商场决定适当降价,经调查发现,若每件衬衫降价1元,则商场平均每天可多售出2件,若商场每天要盈利1200元,每件衬衫应降价多少元?
有A,B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B 布袋中有三个完全相同的小球,分别标有数字-1,-2和-3.小明从A布袋中随机取出一个小球,记录其标有的数字为x,再从B布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点Q的一个坐标为 .
.
(1)用列表或画树状图的方法写出点Q的所有可能坐标;
(2)求点Q落在抛物线y=x2-2x-1上的概率.
抛物线 交
交 轴于点A,交
轴于点A,交 轴 正半轴于点B.
轴 正半轴于点B.
(1)求直线AB对应的函数关系式;
(2)写出当 时,x的取值范围。
时,x的取值范围。
如图,抛物线 经过点A(0,3)、B(-1,0),请解答下列问题:
经过点A(0,3)、B(-1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为D,与 轴的另一交点为C,对称轴交
轴的另一交点为C,对称轴交 轴于点E,连接BD,求
轴于点E,连接BD,求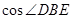
如图,四边形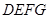 是
是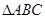 的内接矩形,如果
的内接矩形,如果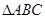 的高线
的高线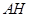 长
长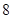
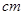 ,底边
,底边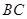 长
长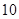
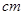 ,设
,设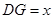
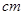 ,
,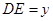
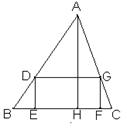
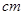 ,
,
(1)求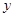 关于
关于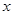 的函数关系式;
的函数关系式;
(2)当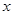 为何值时, 四边形
为何值时, 四边形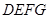 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?
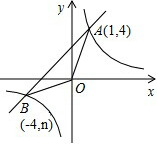
已知,如图,反比例函数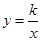 的图像与一次函数
的图像与一次函数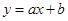 的图像相交于点
的图像相交于点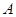
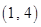 、
、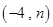 ,
,
(1)试确定这两个函数的表达式;
(2)求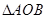 的面积;
的面积;
(3)直接写出使反比例函数的值大于一次函数的值的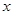 的取值范围.
的取值范围.