如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、DE的长度关系及所在直线的位置关系:
(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系(直接写出答案);
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α得到图2,图3的情 形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
(2)在第(1)题图2中,连接DG、BE,且AB=3,EF=2,求BE2+DG2的值.
如图,AB是⊙O的直径,AC和BD是它的两条切线,CO平分∠ACD.
(1)求证:CD是⊙O的切线;(2)若AC=2,BC=3,求AB的长.
小明和小刚玩“石头、剪刀、布”的游戏,每一局游戏双方各自随机做出“石头”、“剪刀”、“布”三种手势的一种,规定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,相同的手势是和局.
(1)用树形图或列表法计算在一局游戏中两人获胜的概率各是多少?
(2)如果两人约定:只要谁率先胜两局,就成了游戏的赢家.用树形图或列表法求只进行两局游戏便能确定赢家的概率.
如图,海中有一小岛B,它的周围15海里内有暗礁.有一货轮以30海里/时的速度向正北航行半小时后到达C处,发现B岛在它的东北方向.问货轮继续向北航行有无触礁的危险?(参考数据: )
)
某市青少年宫准备在七月一日组织市区部分学校的中小学生到本市A,B,C,D,E五个红色旅游景区“一日游”,每名学生只能在五个景区中任选一个.为估算到各景区旅游的人数,青少年宫随机抽取这些学校的部分学生,进行了“五个红色景区,你最想去哪里”的问卷调查,在统计了所有的调查问卷后将结果绘制成如图所示的统计图.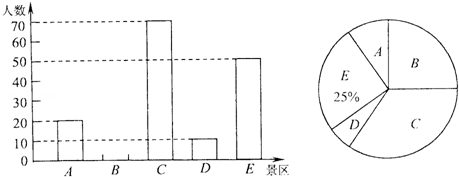
(1)求参加问卷调查的学生数,并将条形统计图补充完整;
(2)若参加“一日游”的学生为1000人,请估计到C景区旅游的人数.
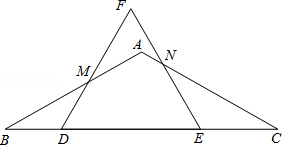
如图,在△ABC中,AB=AC,∠B=30°,BC=8,D在边BC上,E在线段DC上,DE=4,△DEF是等边三角形,边DF交边AB于点M,边EF交边AC于点N.
(1)求证:△BMD∽△CNE;
(2)当BD为何值时,以M为圆心,以MF为半径的圆与BC相切?
(3)设BD=x,五边形ANEDM的面积为y,求y与x之间的函数解析式(要求写出自变量x的取值范围);当x为何值时,y有最大值?并求y的最大值.