学校为了学生的身体健康,每天开展体育活动一小时,开设排球、篮球、羽毛球、体操课.学生可根据自己的爱好任选其中一项,老师根据学生报名情况进行了统计,并绘制 了右边尚未完成的扇形统计图和频数分布直方图,请你结合图中的信息,解答下列问题:
了右边尚未完成的扇形统计图和频数分布直方图,请你结合图中的信息,解答下列问题:
(1)该校学生报名总人数有多少人?
(2)从表中可知选羽毛球的学生有多少人?选排球和篮球的人数分别占报名总人数的百分之几?
(3)将两个统计图补充完整.
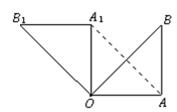
如图所示,在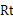 △
△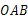 中,
中,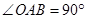 ,
,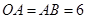 ,将
,将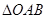 绕点
绕点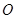 沿逆时针方向旋转
沿逆时针方向旋转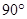 得到
得到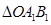 .
.
(1)线段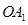 的长是,
的长是,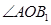 的度数是;
的度数是;
(2)连接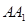 ,求证:四边形
,求证:四边形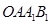 是平行四边形.
是平行四边形.
已知关于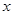 的方程
的方程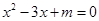 的一个根是另一个根的2倍,求
的一个根是另一个根的2倍,求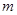 的值.
的值.
小昆和小明玩摸牌游戏,游戏规则如下:有3张背面完全相同,牌面标有数字1、2、3的纸牌,将纸牌洗匀后背面朝上放在桌面上,随机抽出一张,记下牌面数字,放回后洗匀再随机抽出一张。
(1)请用画树形图或列表的方法(只选其中一种),
表示出两次抽出的纸牌数字可能出现的所有结果;
(2)若规定:两次抽出的纸牌数字之和为奇数,则小昆获胜;两次抽出的纸牌数字之和为偶数,则小明获胜。这个游戏公平吗?为什么?
为落实素质教育要求,促进学生全面发展,某市某中学2009年投资11万元新增一批电脑,计划以后每年以相同的增长率进行投资,2011年投资18.59万元。
(1)求该学校为新增电脑投资的年平均增长率;
(2)从2009年到2011年,该中学三年为新增电脑共投资多少万元?
如图,水平放置的一个油管的截面半径为13cm,其中有油部分油面宽AB为24cm,求截面上有油部分油面高CD。