已知抛物线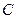 :
: 的顶点在坐标轴上.
的顶点在坐标轴上.
(1)求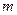 的值;
的值;
(2) 时,抛物线
时,抛物线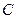 向下平移
向下平移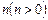 个单位后与抛物线
个单位后与抛物线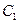 :
: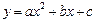 关于
关于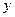 轴对称,且
轴对称,且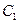 过点
过点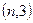 ,求
,求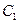 的函数关系式;
的函数关系式;
(3)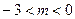 时,抛物线
时,抛物线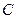 的顶点为
的顶点为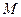 ,且过点
,且过点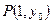 .问在直线
.问在直线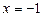 上是否存在一点
上是否存在一点 使得△
使得△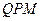 的周长最小,如果存在,求出点
的周长最小,如果存在,求出点 的坐标, 如果不存在,请说明理由.
的坐标, 如果不存在,请说明理由.
将下列命题改写成“如果…那么…”的形式.
(1)同位角相等,两直线平行;
(2)在同一平面内,垂直于同一直线的两直线平行.
举反例说明下列命题是假命题.
(1)如果a+b>0,那么a>0,b>0;
(2)无限小数是无理数;
(3)两直线被第三条直线所截,同位角相等.
写出下列命题的逆命题,并判断其真假:
(1)若a=b,则a3=b3;
(2)个位数是0的数能被2整除.
写出下列命题的条件和结论,并指出它是真命题还是假命题:
(1)有一个角是60°的等腰三角形是等边三角形;
(2)等腰三角形底边上的高和底边上的中线、顶角的平分线互相重合.
把命题改写成”如果…那么…”的形式.
(1)对顶角相等.
(2)两直线平行,同位角相等.
(3)等角的余角相等.