(本小题满分14分)
已知函数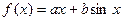 ,当
,当 时,
时, 取得极
取得极 小值
小值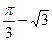 .
.
(1)求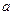 ,
,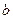 的值;
的值;
(2)设直线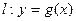 ,曲线
,曲线 .若直线
.若直线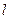
 与曲线
与曲线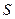 同时满足下列两个条件:
同时满足下列两个条件:
①直线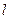 与曲线
与曲线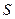 相切且至少有两个
相切且至少有两个 切点;
切点;
②对任意 都有
都有 .则称直线
.则称直线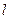 为曲线
为曲线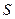 的“上夹线”.
的“上夹线”.
试证明:直线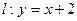 是曲线
是曲线 的“上夹线”.
的“上夹线”.
(3)记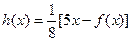 ,设
,设 是方程
是方程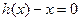 的实数
的实数 根,若对于
根,若对于 定义域中任意的
定义域中任意的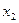 、
、 ,当
,当 ,且
,且 时,问是否存在一个最小的正整数
时,问是否存在一个最小的正整数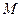 ,使得
,使得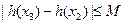 恒成立,若存在请求出
恒成立,若存在请求出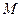 的值;若不存在请说明理由.
的值;若不存在请说明理由.
已知某校5个学生的数学和物理成绩如下表
(1)假设在对这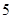 名学生成绩进行统计时,把这
名学生成绩进行统计时,把这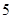 名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有
名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有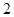 名学生的物理成绩是自己的实际分数的概率是多少?
名学生的物理成绩是自己的实际分数的概率是多少?
(2)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系的,在上述表格是正确的前提下,用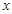 表示数学成绩,用
表示数学成绩,用 表示物理成绩,求
表示物理成绩,求 与
与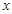 的回归方程;
的回归方程;
(3)利用残差分析回归方程的拟合效果,若残差和在 范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
参考数据和公式: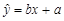 ,其中
,其中 ,
, ;
;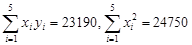 ,残差和公式为:
,残差和公式为:
一厂家向用户提供的一箱产品共10件,其中有2件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品(1)求这箱产品被用户接收的概率;
(2)记抽检的产品件数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
已知在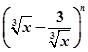 的展开式中,第7项为常数项,
的展开式中,第7项为常数项,
(1)求n的值;
(2)求展开式中所有的有理项.
已知一袋有2个白球和4个黑球。
(1)采用不放回地从袋中摸球(每次摸一球),4次摸球,求恰好摸到2个黑球的概率;
(2)采用有放回从袋中摸球(每次摸一球),4次摸球,令X表示摸到黑球次数,
求X的分布列和期望.
如图,圆O的直径AB=10,弦DE⊥AB于点H, HB="2" .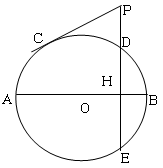
(1)求DE的长;
(2)延长ED到P,过P作圆O的切线,切点为C,若PC=2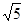 ,求PD的长.
,求PD的长.