如图,直二面角D—AB—E中,四 边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.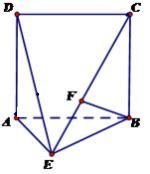
(Ⅰ)求证:AE⊥平面BCE;
(Ⅱ)求点D到平面ACE的距离。
已知 ,
, ,设
,设 .
. (1)求函数
(1)求函数 的最小正周期及其单调递增区间;
的最小正周期及其单调递增区间;
(2)若 分别是锐角
分别是锐角 的内角
的内角 的对边,且
的对边,且 ,
, ,试求
,试求 的面积
的面积 .
.
已知 其中
其中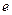 是自然常数,
是自然常数,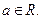
(1)讨论 时,
时, 
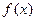 的单调性、极值;
的单调性、极值;
(2)求证:在(1)的条件下,
(3)是否存在实数 ,使
,使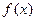 的最小值是3,如果存在,求出
的最小值是3,如果存在,求出 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30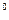 ,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.
,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.
(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)设过点D的直线l与曲线C相交于不同的两点E、F.若△OE F的面积不小于2
F的面积不小于2 ,求直线l斜率的取值范围.
,求直线l斜率的取值范围.
如图,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面A BCD,O是BC中点,AO交BD于E.
BCD,O是BC中点,AO交BD于E.
(1)求证:PA⊥BD;
(2)求二面角P-DC-B的大小;
(3)求证:平面PAD⊥平面PAB.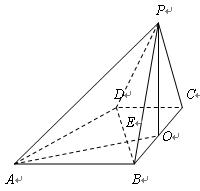
数列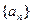 中,
中, .
.
(1)若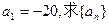 的通项公式
的通项公式 ;
;
(2)设 的最小值.
的最小值.