长度L=0.4m的细线,拴着一个质量m=0.4kg的小球,在竖直平面内作圆周运动,小球运动到最低点时离地面高度h=0.8m,此时细线受到的拉力F=13N,g取10m/s2,求:
(1)小球在最低点速度的大小;
(2)若小球运动到最低点时细线恰好断裂,则小球着地时速度为多大?
一平行金属导轨水平面内固定,导轨间距L=0.5m,导轨右端接有电阻RL=4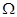 小灯泡,导轨电阻不计,如图甲。在导轨的MNQP矩形区域内有竖直向上的磁场,MN、PQ间距d=3m,此区域磁感应强度B随时间t变化规律如图乙所示,垂直导轨跨接一质量m=1kg的金属杆,其电阻r=1
小灯泡,导轨电阻不计,如图甲。在导轨的MNQP矩形区域内有竖直向上的磁场,MN、PQ间距d=3m,此区域磁感应强度B随时间t变化规律如图乙所示,垂直导轨跨接一质量m=1kg的金属杆,其电阻r=1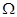 ,金属杆与导轨间的动摩擦因数为
,金属杆与导轨间的动摩擦因数为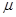 =0.2,在t=0时刻,给金属棒以速度v0=2m/s,同时施加一向右的外力F,使其从GH处向右运动,在0--2s内小灯发光亮度始终没变化,求:
=0.2,在t=0时刻,给金属棒以速度v0=2m/s,同时施加一向右的外力F,使其从GH处向右运动,在0--2s内小灯发光亮度始终没变化,求: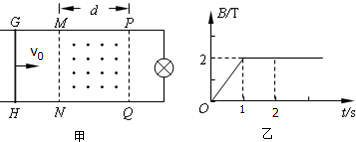
(1)通过计算分析2s内金属杆的运动情况;
(2)计算2s内外力F的大小;
(3)计算2s内整个系统产生热量。
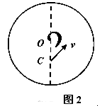
离子推进器是太空飞行器常用的动力系统,某种推进器设计的简化原理如图1所示,截面半径为R的圆柱腔分为两个工作区。I为电离区,将氙气电离获得1价正离子II为加速区,长度为L,两端加有电压,形成轴向的匀强电场。I区产生的正离子以接近0的初速度进入II区,被加速后以速度vM从右侧喷出。I区内有轴向的匀强磁场,磁感应强度大小为B,在离轴线R/2处的C点持续射出一定速度范围的电子。假设射出的电子仅在垂直于轴线的截面上运动,截面如图2所示(从左向右看)。电子的初速度方向与中心O点和C点的连线成α角(0<α<90o)。推进器工作时,向I区注入稀薄的氙气。电子使氙气电离的最小速度为v0,电子在I区内不与器壁相碰且能到达的区域越大,电离效果越好。已知离子质量为M;电子质量为m,电量为e。(电子碰到器壁即被吸收,不考虑电子间的碰撞)。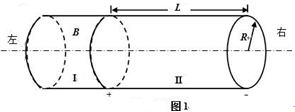
(1)求II区的加速电压及离子的加速度大小;
(2)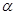 为90o时,要取得好的电离效果,求射出的电子速率v的范围;
为90o时,要取得好的电离效果,求射出的电子速率v的范围;
(3)要取得好的电离效果,求射出的电子最大速率vm与α的关系。
光滑水平面上,用轻质弹簧连接的质量为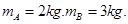 的A、B两物体都以
的A、B两物体都以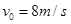 的速度向右运动,此时弹簧处于原长状态。质量为
的速度向右运动,此时弹簧处于原长状态。质量为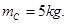 的物体C静止在前方,如图所示,B与C碰撞后粘合在一起运动,求:
的物体C静止在前方,如图所示,B与C碰撞后粘合在一起运动,求:
①B、C碰撞刚结束时的瞬时速度的大小;
②在以后的运动过程中,弹簧的最大弹性势能。
如图所示是一列沿x轴正向传播的简谐横波在t=0.25s时刻的波形图,已知波的传播速度v=4m/s。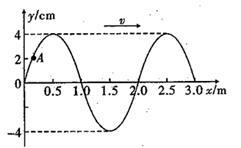
①画出x=2.0m处质点的振动图像(至少画出一个周期);
②求x=2.5m处质点在0~4.5s内通过的路程及t=4.5s时的位移;
③此时A点的纵坐标为2cm,试求从图示时刻开始经过多少时间A点第三次出现波峰?
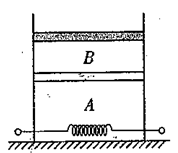
如图所示,一个绝热的气缸(气缸足够高)竖直放置,内有一个绝热且光滑的活塞,中间有一个固定的导热性良好的隔板,隔板将气缸分成两部分,分别密封着两部分理想气体A和B。活塞的质量m=8kg,横截面积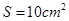 ,与隔板相距h=25cm,现通过电热丝缓慢加热气体,当A气体吸收热量Q=200J时,活塞上升了
,与隔板相距h=25cm,现通过电热丝缓慢加热气体,当A气体吸收热量Q=200J时,活塞上升了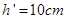 ,此时气体的温度为
,此时气体的温度为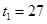 ℃,已知大气压强
℃,已知大气压强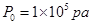 ,重力加速度
,重力加速度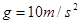 。
。
①加热过程中,若A气体的内能增加了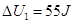 ,求B气体的内能增加量
,求B气体的内能增加量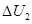 ;
;
②现在停止对气体加热,同时在活塞上缓慢添加沙粒,当活塞恰好回到原来的位置时,A气体的温度为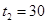 ℃,求此添加砂粒的总质量M。
℃,求此添加砂粒的总质量M。