如图所示是一种自行车上照明用的车头灯发电机的结构示意图,转轴的一端装有一对随轴转动的磁极,另一端装有摩擦小轮.电枢线圈绕在固定的U形铁芯上,自行车车轮转动时,通过摩擦小轮带动磁极转动,使线圈中产生正弦交变电流,给车头灯供电.已知自行车车轮半径r="35" cm,摩擦小轮半径r0="1.00" cm,线圈有n=800匝,线圈框横截面积S="20" cm2,总电阻R1=40Ω.旋转磁极的磁感应强度B="0.010" T,车头灯电阻R2=
10Ω.当车轮转动的角速度ω="8" rad/s时求:
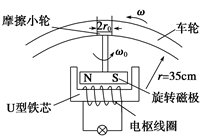
（1）发电机磁极转动的角速度.
（2）车头灯中电流的有效值.
质量为2kg的物体水平推力F的作用下沿水平面做直线运动，一段时间后撤去F,其运动的v-t图象如图所示，g取10m/s2，求
(1)物体与水平面间的动摩擦因数μ;
(2)水平推力F的大小;
(3)0-10s内物体运动位移的大小。
汤姆逊用来测定电子的比荷实验装置如下：真空管内的阴极C发出电子，（不计初速，重力和电子间相互作用）, 经
过A、B间的电场加速后，穿过A、B的中心小孔沿中心轴O/O的方向进入到两块水平正对的长度为L的平行极板D和E间的区域，当极板间不加偏转电压时，电子束打在荧光屏的中心O＇点，形成一个亮点；若在D、E间加上方向向下、场强为E的匀强电场，电子将向上偏转；如果再利用通电线圈在D、E电场区加上一垂
直纸面的匀强磁场（图中未画出），调节磁场的强弱，当磁感应强度的大小为B时，荧光斑恰好回到荧光屏中心。接着再去掉电场，电子向下偏转，偏转角为φ。如图所示，求（1）在图中画出磁场B的方向（2）根据L、E、B和φ，推导电子的比荷的表达式。
在某介质中形成一列简谐横波，该横波上有相距4m的A、B两点，下图所示为A、B两质点的振动图象，若这列波的波长大于2m，求：这列波的波速。
如图所示，质量为M的木框内静止在地面上，劲度系数为k的轻质弹簧一端固定于木框，一质量为m的小球放在该弹簧上，让小球在同一条
竖直线上作简谐运动，在此过程中木框始终没有离开地面。若使小球始终不脱离弹簧，则：
（1）小球的最大振幅A是多大？
（
2）在这个振幅下木框对地面的最大压力是多少？
（3）在这个振幅下弹簧的最大弹性势能是多大？
如图所示，两电阻不计的足够长光滑平行金属导轨与水平面夹角为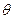
，导轨间距为l，所在平面的正方形区域abcd内存在有界匀强磁场，磁感应强度大小为B，方向垂直于斜面向上。如图所示，将甲、乙两阻值相同，质量均为m的相同金属杆放置在导轨上，甲金属杆处在磁场的上边界，甲、乙相距l。从静止释放两金属杆的同时，在金属杆上施加一个沿着导轨的外力，使甲金属杆在运动过程中始终沿导轨向下做匀加速直线运动，且加速度大小以
，乙金属杆刚进入磁场时做匀速运动。
（1）求每根金属杆的电阻R为多少?
（2）从刚释放金属杆时开始计时，写出从计时开始到甲金属杆离开磁场的过程中外力F随时间t的变化关系式，并说明F的方向。
（3）若从开始释放到两杆到乙金属杆离开磁场，乙金属杆共产生热量Q，试求此过程中外力F对甲做的功。