.
(10分)今年春季，我国云南、贵州等西南地区遇到多少不遇旱灾，“一方有难，八方支援”，为及时灌溉农田，丰收农机公司决定支援上坪村甲、乙、丙三种不同功率柴油发电机共10台(每种至少一台)及配套相同型号抽水机4台、3台、2台，每台抽水机每小时可抽水灌溉农田1亩.现要求所有柴油发电机及配套抽水机同时工作一小时，灌溉农田32亩.
(1)设甲种柴油发电机数量为x台，乙种柴油发电机数量为y台.
①用含x、y的式子表示丙种柴油发电机的数量；
②求出y与x的关系式；
(2)已知甲、乙、丙柴油发电机每台每小时费用分别为130元、120元、100元，应如何安排三种柴油发电机的数量，既能按要求抽水灌溉，同时柴油发电机总费用W最少？
（遂宁）如图，▱ABCD中，点E，F在对角线BD上，且BE=DF，求证：
（1）AE=CF；
（2）四边形AECF是平行四边形．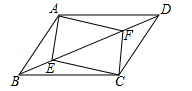
（自贡）在▱ABCD中，∠BCD的平分线与BA的延长线相交于点E，BH⊥EC于点H，求证：CH=EH．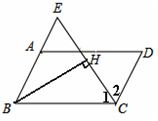
（内江）（本小题满分9分）如图，将▱ABCD的边AB延长至点E，使AB=BE，连接DE，EC，DE交BC于点O．
（1）求证：△ABD≌△BEC；
（2）连接BD，若∠BOD=2∠A，求证：四边形BECD是矩形．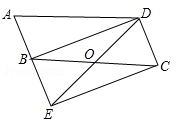
（内江）如图，在△ACE中，CA=CE，∠CAE=30°，⊙O经过点C，且圆的直径AB在线段AE上．
（1）试说明CE是⊙O的切线；
（2）若△ACE中AE边上的高为h，试用含h的代数式表示⊙O的直径AB；
（3）设点D是线段AC上任意一点（不含端点），连接OD，当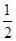
CD+OD的最小值为6时，求⊙O的直径AB的长．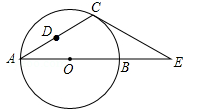
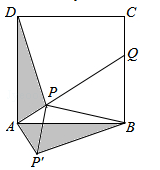
（南充）如图，点P是正方形ABCD内一点，点P到点A、B和D的距离分别为1，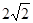
，
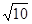，△ADP沿点A旋转至△ABP′，连结PP′，并延长AP与BC相交于点Q．
（1）求证：△APP′是等腰直角三角形；
（2）求∠BPQ的大小；
（3）求CQ的长．